Dealing with heteroskedasticity; regression with robust standard errors using R
RFirst of all, is it heteroskedasticity or heteroscedasticity? According to McCulloch (1985), heteroskedasticity is the proper spelling, because when transliterating Greek words, scientists use the Latin letter k in place of the Greek letter κ (kappa). κ sometimes is transliterated as the Latin letter c, but only when these words entered the English language through French, such as scepter.
Now that this is out of the way, we can get to the meat of this blogpost (foreshadowing pun). A random variable is said to be heteroskedastic, if its variance is not constant. For example, the variability of expenditures may increase with income. Richer families may spend a similar amount on groceries as poorer people, but some rich families will sometimes buy expensive items such as lobster. The variability of expenditures for rich families is thus quite large. However, the expenditures on food of poorer families, who cannot afford lobster, will not vary much. Heteroskedasticity can also appear when data is clustered; for example, variability of expenditures on food may vary from city to city, but is quite constant within a city.
To illustrate this, let’s first load all the packages needed for this blog post:
library(robustbase)
library(tidyverse)
library(sandwich)
library(lmtest)
library(modelr)
library(broom)First, let’s load and prepare the data:
data("education")
education <- education %>%
rename(residents = X1,
per_capita_income = X2,
young_residents = X3,
per_capita_exp = Y,
state = State) %>%
mutate(region = case_when(
Region == 1 ~ "northeast",
Region == 2 ~ "northcenter",
Region == 3 ~ "south",
Region == 4 ~ "west"
)) %>%
select(-Region)I will be using the education data set from the {robustbase} package. I renamed some columns
and changed the values of the Region column. Now, let’s do a scatterplot of per capita expenditures
on per capita income:
ggplot(education, aes(per_capita_income, per_capita_exp)) +
geom_point() +
theme_dark()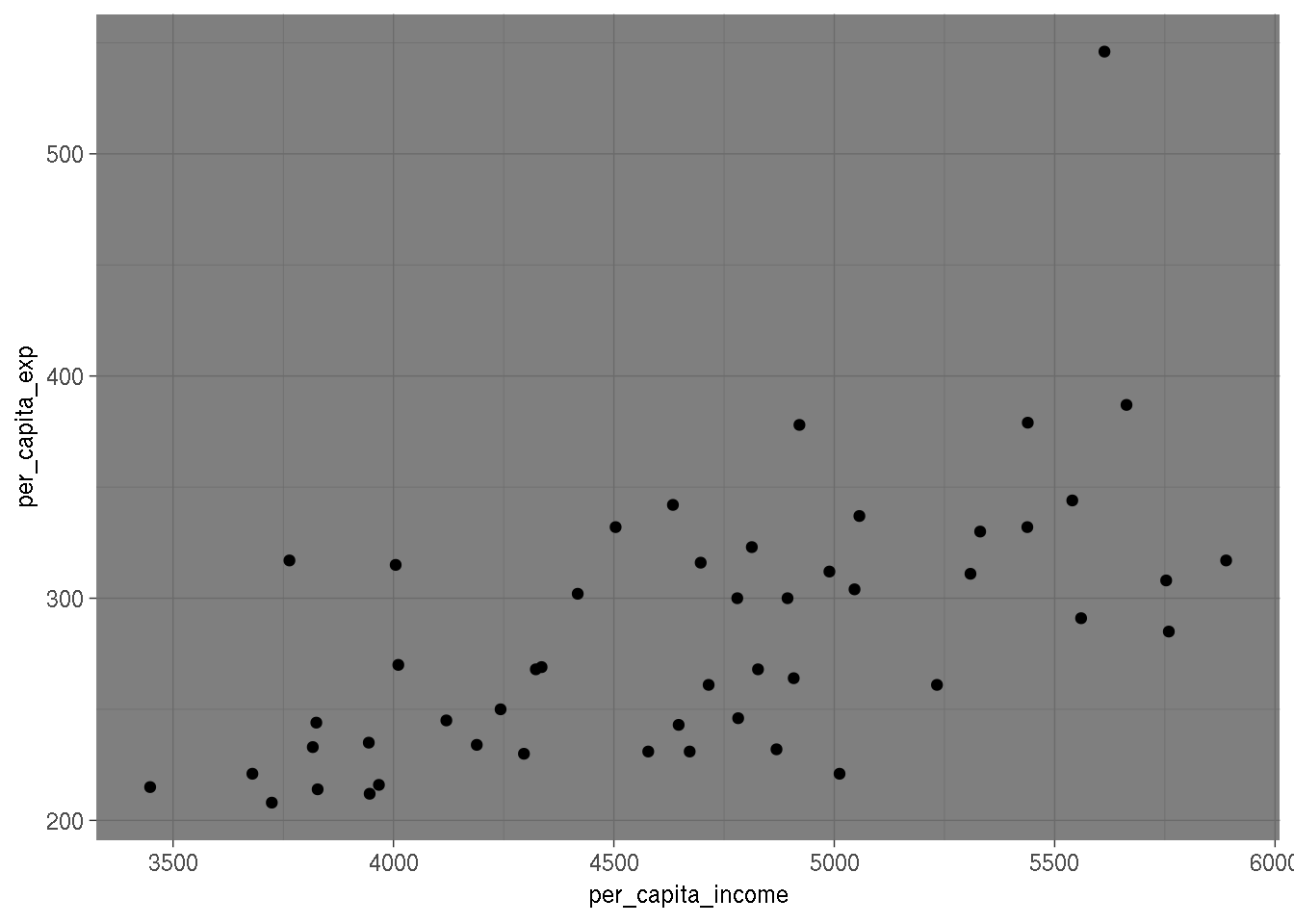
It would seem that, as income increases, variability of expenditures increases too. Let’s look
at the same plot by region:
ggplot(education, aes(per_capita_income, per_capita_exp)) +
geom_point() +
facet_wrap(~region) +
theme_dark()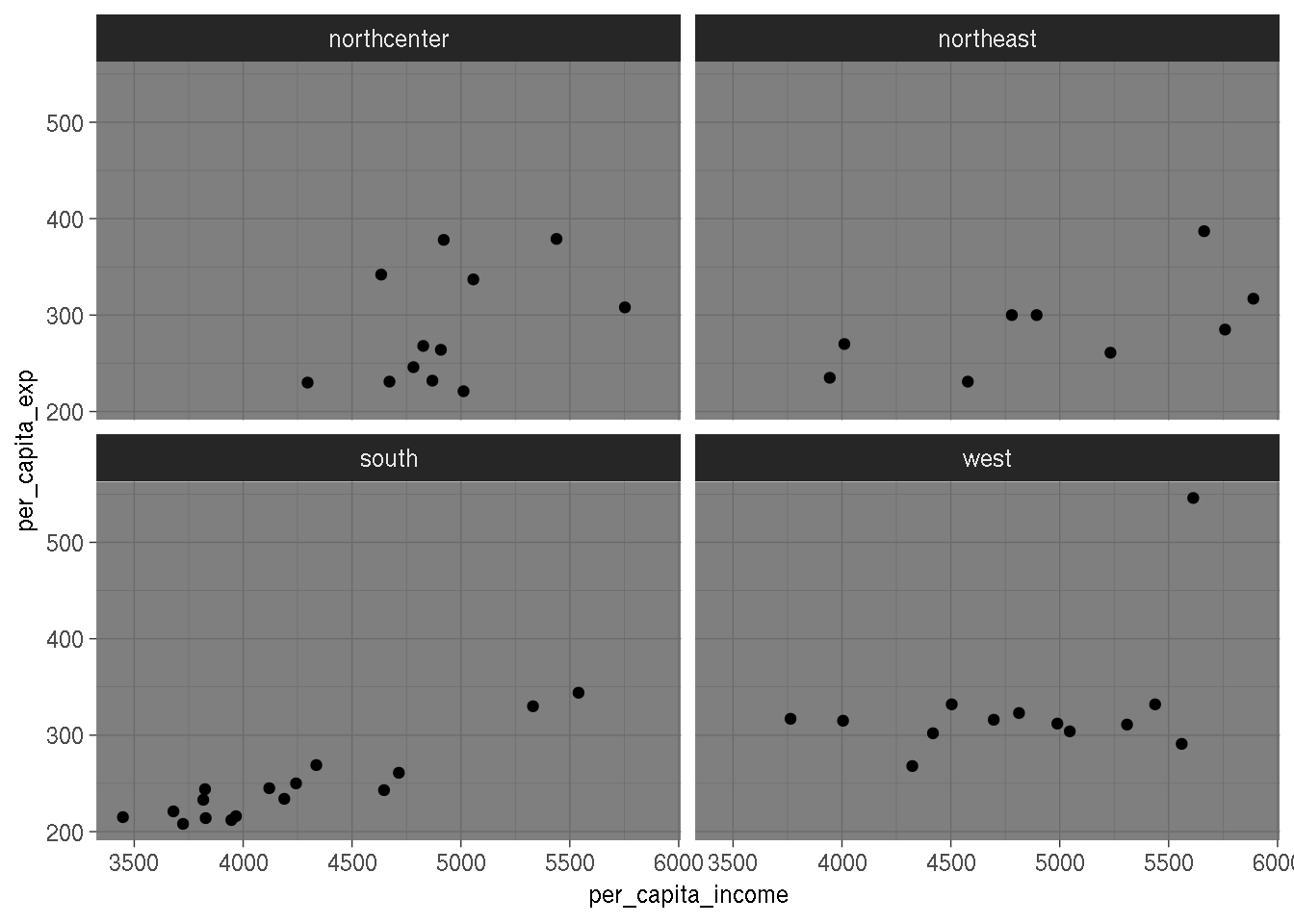
I don’t think this shows much; it would seem that observations might be clustered, but there are not enough observations to draw any conclusion from this plot (in any case, drawing conclusions from only plots is dangerous).
Let’s first run a good ol’ linear regression:
lmfit <- lm(per_capita_exp ~ region + residents + young_residents + per_capita_income, data = education)
summary(lmfit)##
## Call:
## lm(formula = per_capita_exp ~ region + residents + young_residents +
## per_capita_income, data = education)
##
## Residuals:
## Min 1Q Median 3Q Max
## -77.963 -25.499 -2.214 17.618 89.106
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -467.40283 142.57669 -3.278 0.002073 **
## regionnortheast 15.72741 18.16260 0.866 0.391338
## regionsouth 7.08742 17.29950 0.410 0.684068
## regionwest 34.32416 17.49460 1.962 0.056258 .
## residents -0.03456 0.05319 -0.650 0.519325
## young_residents 1.30146 0.35717 3.644 0.000719 ***
## per_capita_income 0.07204 0.01305 5.520 1.82e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 39.88 on 43 degrees of freedom
## Multiple R-squared: 0.6292, Adjusted R-squared: 0.5774
## F-statistic: 12.16 on 6 and 43 DF, p-value: 6.025e-08Let’s test for heteroskedasticity using the Breusch-Pagan test that you can find in the {lmtest}
package:
bptest(lmfit)##
## studentized Breusch-Pagan test
##
## data: lmfit
## BP = 17.921, df = 6, p-value = 0.006432This test shows that we can reject the null that the variance of the residuals is constant,
thus heteroskedacity is present. To get the correct standard errors, we can use the vcovHC()
function from the {sandwich} package (hence the choice for the header picture of this post):
lmfit %>%
vcovHC() %>%
diag() %>%
sqrt()## (Intercept) regionnortheast regionsouth regionwest
## 311.31088691 25.30778221 23.56106307 24.12258706
## residents young_residents per_capita_income
## 0.09184368 0.68829667 0.02999882By default vcovHC() estimates a heteroskedasticity consistent (HC) variance covariance
matrix for the parameters. There are several ways to estimate such a HC matrix, and by default
vcovHC() estimates the “HC3” one. You can refer to Zeileis (2004)
for more details.
We see that the standard errors are much larger than before! The intercept and regionwest variables
are not statistically significant anymore.
You can achieve the same in one single step:
coeftest(lmfit, vcov = vcovHC(lmfit))##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -467.402827 311.310887 -1.5014 0.14056
## regionnortheast 15.727405 25.307782 0.6214 0.53759
## regionsouth 7.087424 23.561063 0.3008 0.76501
## regionwest 34.324157 24.122587 1.4229 0.16198
## residents -0.034558 0.091844 -0.3763 0.70857
## young_residents 1.301458 0.688297 1.8908 0.06540 .
## per_capita_income 0.072036 0.029999 2.4013 0.02073 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1It’s is also easy to change the estimation method for the variance-covariance matrix:
coeftest(lmfit, vcov = vcovHC(lmfit, type = "HC0"))##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -467.402827 172.577569 -2.7084 0.009666 **
## regionnortheast 15.727405 20.488148 0.7676 0.446899
## regionsouth 7.087424 17.755889 0.3992 0.691752
## regionwest 34.324157 19.308578 1.7777 0.082532 .
## residents -0.034558 0.054145 -0.6382 0.526703
## young_residents 1.301458 0.387743 3.3565 0.001659 **
## per_capita_income 0.072036 0.016638 4.3296 8.773e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1As I wrote above, by default, the type argument is equal to “HC3”.
Another way of dealing with heteroskedasticity is to use the lmrob() function from the
{robustbase} package. This package is quite interesting, and offers quite a lot of functions
for robust linear, and nonlinear, regression models. Running a robust linear regression
is just the same as with lm():
lmrobfit <- lmrob(per_capita_exp ~ region + residents + young_residents + per_capita_income,
data = education)
summary(lmrobfit)##
## Call:
## lmrob(formula = per_capita_exp ~ region + residents + young_residents + per_capita_income,
## data = education)
## \--> method = "MM"
## Residuals:
## Min 1Q Median 3Q Max
## -57.074 -14.803 -0.853 24.154 174.279
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -156.37169 132.73828 -1.178 0.24526
## regionnortheast 20.64576 26.45378 0.780 0.43940
## regionsouth 10.79695 29.42746 0.367 0.71549
## regionwest 45.22589 33.07950 1.367 0.17867
## residents 0.03406 0.04412 0.772 0.44435
## young_residents 0.57896 0.25512 2.269 0.02832 *
## per_capita_income 0.04328 0.01442 3.000 0.00447 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Robust residual standard error: 26.4
## Multiple R-squared: 0.6235, Adjusted R-squared: 0.571
## Convergence in 24 IRWLS iterations
##
## Robustness weights:
## observation 50 is an outlier with |weight| = 0 ( < 0.002);
## 7 weights are ~= 1. The remaining 42 ones are summarized as
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.05827 0.85200 0.93870 0.85250 0.98700 0.99790
## Algorithmic parameters:
## tuning.chi bb tuning.psi refine.tol
## 1.548e+00 5.000e-01 4.685e+00 1.000e-07
## rel.tol scale.tol solve.tol eps.outlier
## 1.000e-07 1.000e-10 1.000e-07 2.000e-03
## eps.x warn.limit.reject warn.limit.meanrw
## 1.071e-08 5.000e-01 5.000e-01
## nResample max.it best.r.s k.fast.s k.max
## 500 50 2 1 200
## maxit.scale trace.lev mts compute.rd fast.s.large.n
## 200 0 1000 0 2000
## psi subsampling cov
## "bisquare" "nonsingular" ".vcov.avar1"
## compute.outlier.stats
## "SM"
## seed : int(0)This however, gives you different estimates than when fitting a linear regression model. The estimates should be the same, only the standard errors should be different. This is because the estimation method is different, and is also robust to outliers (at least that’s my understanding, I haven’t read the theoretical papers behind the package yet).
Finally, it is also possible to bootstrap the standard errors. For this I will use the
bootstrap() function from the {modelr} package:
resamples <- 100
boot_education <- education %>%
modelr::bootstrap(resamples)Let’s take a look at the boot_education object:
boot_education## # A tibble: 100 x 2
## strap .id
## <list> <chr>
## 1 <resample> 001
## 2 <resample> 002
## 3 <resample> 003
## 4 <resample> 004
## 5 <resample> 005
## 6 <resample> 006
## 7 <resample> 007
## 8 <resample> 008
## 9 <resample> 009
## 10 <resample> 010
## # … with 90 more rowsThe column strap contains resamples of the original data. I will run my linear regression
from before on each of the resamples:
(
boot_lin_reg <- boot_education %>%
mutate(regressions =
map(strap,
~lm(per_capita_exp ~ region + residents +
young_residents + per_capita_income,
data = .)))
)## # A tibble: 100 x 3
## strap .id regressions
## <list> <chr> <list>
## 1 <resample> 001 <lm>
## 2 <resample> 002 <lm>
## 3 <resample> 003 <lm>
## 4 <resample> 004 <lm>
## 5 <resample> 005 <lm>
## 6 <resample> 006 <lm>
## 7 <resample> 007 <lm>
## 8 <resample> 008 <lm>
## 9 <resample> 009 <lm>
## 10 <resample> 010 <lm>
## # … with 90 more rowsI have added a new column called regressions which contains the linear regressions on each
bootstrapped sample. Now, I will create a list of tidied regression results:
(
tidied <- boot_lin_reg %>%
mutate(tidy_lm =
map(regressions, broom::tidy))
)## # A tibble: 100 x 4
## strap .id regressions tidy_lm
## <list> <chr> <list> <list>
## 1 <resample> 001 <lm> <tibble [7 × 5]>
## 2 <resample> 002 <lm> <tibble [7 × 5]>
## 3 <resample> 003 <lm> <tibble [7 × 5]>
## 4 <resample> 004 <lm> <tibble [7 × 5]>
## 5 <resample> 005 <lm> <tibble [7 × 5]>
## 6 <resample> 006 <lm> <tibble [7 × 5]>
## 7 <resample> 007 <lm> <tibble [7 × 5]>
## 8 <resample> 008 <lm> <tibble [7 × 5]>
## 9 <resample> 009 <lm> <tibble [7 × 5]>
## 10 <resample> 010 <lm> <tibble [7 × 5]>
## # … with 90 more rowsbroom::tidy() creates a data frame of the regression results. Let’s look at one of these:
tidied$tidy_lm[[1]]## # A tibble: 7 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) -571. 109. -5.22 4.92e- 6
## 2 regionnortheast -48.0 17.2 -2.80 7.71e- 3
## 3 regionsouth -21.3 15.1 -1.41 1.66e- 1
## 4 regionwest 1.88 13.9 0.135 8.93e- 1
## 5 residents -0.134 0.0608 -2.21 3.28e- 2
## 6 young_residents 1.50 0.308 4.89 1.47e- 5
## 7 per_capita_income 0.100 0.0125 8.06 3.85e-10This format is easier to handle than the standard lm() output:
tidied$regressions[[1]]##
## Call:
## lm(formula = per_capita_exp ~ region + residents + young_residents +
## per_capita_income, data = .)
##
## Coefficients:
## (Intercept) regionnortheast regionsouth
## -571.0568 -48.0018 -21.3019
## regionwest residents young_residents
## 1.8808 -0.1341 1.5042
## per_capita_income
## 0.1005Now that I have all these regression results, I can compute any statistic I need. But first, let’s transform the data even further:
list_mods <- tidied %>%
pull(tidy_lm)list_mods is a list of the tidy_lm data frames. I now add an index and
bind the rows together (by using map2_df() instead of map2()):
mods_df <- map2_df(list_mods,
seq(1, resamples),
~mutate(.x, resample = .y))Let’s take a look at the final object:
head(mods_df, 25)## # A tibble: 25 x 6
## term estimate std.error statistic p.value resample
## <chr> <dbl> <dbl> <dbl> <dbl> <int>
## 1 (Intercept) -571. 109. -5.22 4.92e- 6 1
## 2 regionnortheast -48.0 17.2 -2.80 7.71e- 3 1
## 3 regionsouth -21.3 15.1 -1.41 1.66e- 1 1
## 4 regionwest 1.88 13.9 0.135 8.93e- 1 1
## 5 residents -0.134 0.0608 -2.21 3.28e- 2 1
## 6 young_residents 1.50 0.308 4.89 1.47e- 5 1
## 7 per_capita_income 0.100 0.0125 8.06 3.85e-10 1
## 8 (Intercept) -97.2 145. -0.672 5.05e- 1 2
## 9 regionnortheast -1.48 10.8 -0.136 8.92e- 1 2
## 10 regionsouth 12.5 11.4 1.09 2.82e- 1 2
## # … with 15 more rowsNow this is a very useful format, because I now can group by the term column and compute any
statistics I need, in the present case the standard deviation:
(
r.std.error <- mods_df %>%
group_by(term) %>%
summarise(r.std.error = sd(estimate))
)## # A tibble: 7 x 2
## term r.std.error
## <chr> <dbl>
## 1 (Intercept) 220.
## 2 per_capita_income 0.0197
## 3 regionnortheast 24.5
## 4 regionsouth 21.1
## 5 regionwest 22.7
## 6 residents 0.0607
## 7 young_residents 0.498We can append this column to the linear regression model result:
lmfit %>%
broom::tidy() %>%
full_join(r.std.error) %>%
select(term, estimate, std.error, r.std.error)## Joining, by = "term"## # A tibble: 7 x 4
## term estimate std.error r.std.error
## <chr> <dbl> <dbl> <dbl>
## 1 (Intercept) -467. 143. 220.
## 2 regionnortheast 15.7 18.2 24.5
## 3 regionsouth 7.09 17.3 21.1
## 4 regionwest 34.3 17.5 22.7
## 5 residents -0.0346 0.0532 0.0607
## 6 young_residents 1.30 0.357 0.498
## 7 per_capita_income 0.0720 0.0131 0.0197As you see, using the whole bootstrapping procedure is longer than simply using either one of the first two methods. However, this procedure is very flexible and can thus be adapted to a very large range of situations. Either way, in the case of heteroskedasticity, you can see that results vary a lot depending on the procedure you use, so I would advise to use them all as robustness tests and discuss the differences.
If you found this blog post useful, you might want to follow me on twitter for blog post updates.
