A tutorial on tidy cross-validation with R
RIntroduction
This blog posts will use several packages from the
{tidymodels} collection of packages, namely
{recipes},
{rsample} and
{parsnip} to train a random forest the tidy way. I will
also use {mlrMBO} to tune the hyper-parameters of the random forest.
Set up
Let’s load the needed packages:
library("tidyverse")
library("tidymodels")
library("parsnip")
library("brotools")
library("mlbench")Load the data, included in the {mlrbench} package:
data("BostonHousing2")I will train a random forest to predict the housing price, which is the cmedv column:
head(BostonHousing2)## town tract lon lat medv cmedv crim zn indus chas nox
## 1 Nahant 2011 -70.9550 42.2550 24.0 24.0 0.00632 18 2.31 0 0.538
## 2 Swampscott 2021 -70.9500 42.2875 21.6 21.6 0.02731 0 7.07 0 0.469
## 3 Swampscott 2022 -70.9360 42.2830 34.7 34.7 0.02729 0 7.07 0 0.469
## 4 Marblehead 2031 -70.9280 42.2930 33.4 33.4 0.03237 0 2.18 0 0.458
## 5 Marblehead 2032 -70.9220 42.2980 36.2 36.2 0.06905 0 2.18 0 0.458
## 6 Marblehead 2033 -70.9165 42.3040 28.7 28.7 0.02985 0 2.18 0 0.458
## rm age dis rad tax ptratio b lstat
## 1 6.575 65.2 4.0900 1 296 15.3 396.90 4.98
## 2 6.421 78.9 4.9671 2 242 17.8 396.90 9.14
## 3 7.185 61.1 4.9671 2 242 17.8 392.83 4.03
## 4 6.998 45.8 6.0622 3 222 18.7 394.63 2.94
## 5 7.147 54.2 6.0622 3 222 18.7 396.90 5.33
## 6 6.430 58.7 6.0622 3 222 18.7 394.12 5.21Only keep relevant columns:
boston <- BostonHousing2 %>%
select(-medv, -town, -lon, -lat) %>%
rename(price = cmedv)I remove town, lat and lon because the information contained in the column tract is enough.
To train and evaluate the model’s performance, I split the data in two. One data set, which I call the training set, will be further split into two down below. I won’t touch the second data set, the test set, until the very end.
train_test_split <- initial_split(boston, prop = 0.9)
housing_train <- training(train_test_split)
housing_test <- testing(train_test_split)I want to train a random forest to predict price of houses, but random forests have so-called hyperparameters, which are parameters that cannot be estimated, or learned, from the data. Instead, these parameters have to be chosen by the analyst. In order to choose them, you can use values from the literature that seemed to have worked well (like is done in Macro-econometrics) or you can further split the train set into two, create a grid of hyperparameter, train the model on one part of the data for all values of the grid, and compare the predictions of the models on the second part of the data. You then stick with the model that performed the best, for example, the model with lowest RMSE. The thing is, you can’t estimate the true value of the RMSE with only one value. It’s like if you wanted to estimate the height of the population by drawing one single observation from the population. You need a bit more observations. To approach the true value of the RMSE for a give set of hyperparameters, instead of doing one split, I’ll do 30. I then compute the average RMSE, which implies training 30 models for each combination of the values of the hyperparameters I am interested in.
First, let’s split the training data again, using the mc_cv() function from {rsample} package.
This function implements Monte Carlo cross-validation:
validation_data <- mc_cv(housing_train, prop = 0.9, times = 30)What does validation_data look like?
validation_data## # # Monte Carlo cross-validation (0.9/0.1) with 30 resamples
## # A tibble: 30 x 2
## splits id
## <list> <chr>
## 1 <split [411/45]> Resample01
## 2 <split [411/45]> Resample02
## 3 <split [411/45]> Resample03
## 4 <split [411/45]> Resample04
## 5 <split [411/45]> Resample05
## 6 <split [411/45]> Resample06
## 7 <split [411/45]> Resample07
## 8 <split [411/45]> Resample08
## 9 <split [411/45]> Resample09
## 10 <split [411/45]> Resample10
## # … with 20 more rowsLet’s look further down:
validation_data$splits[[1]]## <411/45/456>The first value is the number of rows of the first set, the second value of the second, and the third was the original amount of values in the training data, before splitting again.
How should we call these two new data sets? The author of {rsample}, Max Kuhn, talks about
the analysis and the assessment sets:
rsample convention for now but I intend on using it everywhere. Reusing training and testing is insane.
— Max Kuhn (@topepos) November 24, 2018
Now, in order to continue I need pre-process the data. I will do this in three steps. The first and the second step are used to center and scale the numeric variables and the third step converts character and factor variables to dummy variables. This is needed because I will train a random forest, which cannot handle factor variables directly. Let’s define a recipe to do that, and start by pre-processing the testing set. I write a wrapper function around the recipe, because I will need to apply this recipe to various data sets:
simple_recipe <- function(dataset){
recipe(price ~ ., data = dataset) %>%
step_center(all_numeric()) %>%
step_scale(all_numeric()) %>%
step_dummy(all_nominal())
}Once the recipe is defined, I can use the prep() function, which estimates the parameters from
the data which are needed to process the data. For example, for centering, prep() estimates
the mean which will then be subtracted from the variables. With bake() the estimates are then
applied on the data:
testing_rec <- prep(simple_recipe(housing_test), testing = housing_test)
test_data <- bake(testing_rec, newdata = housing_test)## Warning: Please use `new_data` instead of `newdata` with `bake`.
## In recipes versions >= 0.1.4, this will cause an error.It is important to split the data before using prep() and bake(), because if not, you will
use observations from the test set in the prep() step, and thus introduce knowledge from the test
set into the training data. This is called data leakage, and must be avoided. This is why it is
necessary to first split the training data into an analysis and an assessment set, and then also
pre-process these sets separately. However, the validation_data object cannot now be used with
recipe(), because it is not a dataframe. No worries, I simply need to write a function that extracts
the analysis and assessment sets from the validation_data object, applies the pre-processing, trains
the model, and returns the RMSE. This will be a big function, at the center of the analysis.
But before that, let’s run a simple linear regression, as a benchmark. For the linear regression, I will not use any CV, so let’s pre-process the training set:
trainlm_rec <- prep(simple_recipe(housing_train), testing = housing_train)
trainlm_data <- bake(trainlm_rec, newdata = housing_train)## Warning: Please use `new_data` instead of `newdata` with `bake`.
## In recipes versions >= 0.1.4, this will cause an error.linreg_model <- lm(price ~ ., data = trainlm_data)
broom::augment(linreg_model, newdata = test_data) %>%
rmse(price, .fitted)## # A tibble: 1 x 3
## .metric .estimator .estimate
## <chr> <chr> <dbl>
## 1 rmse standard 0.438broom::augment() adds the predictions to the test_data in a new column, .fitted. I won’t
use this trick with the random forest, because there is no augment() method for random forests
from the {ranger} which I’ll use. I’ll add the predictions to the data myself.
Ok, now let’s go back to the random forest and write the big function:
my_rf <- function(mtry, trees, split, id){
analysis_set <- analysis(split)
analysis_prep <- prep(simple_recipe(analysis_set), training = analysis_set)
analysis_processed <- bake(analysis_prep, newdata = analysis_set)
model <- rand_forest(mtry = mtry, trees = trees) %>%
set_engine("ranger", importance = 'impurity') %>%
fit(price ~ ., data = analysis_processed)
assessment_set <- assessment(split)
assessment_prep <- prep(simple_recipe(assessment_set), testing = assessment_set)
assessment_processed <- bake(assessment_prep, newdata = assessment_set)
tibble::tibble("id" = id,
"truth" = assessment_processed$price,
"prediction" = unlist(predict(model, new_data = assessment_processed)))
}The rand_forest() function is available from the {parsnip} package. This package provides an
unified interface to a lot of other machine learning packages. This means that instead of having to
learn the syntax of range() and randomForest() and, and… you can simply use the rand_forest()
function and change the engine argument to the one you want (ranger, randomForest, etc).
Let’s try this function:
results_example <- map2_df(.x = validation_data$splits,
.y = validation_data$id,
~my_rf(mtry = 3, trees = 200, split = .x, id = .y))head(results_example)## # A tibble: 6 x 3
## id truth prediction
## <chr> <dbl> <dbl>
## 1 Resample01 0.0235 -0.104
## 2 Resample01 -0.135 -0.0906
## 3 Resample01 -0.378 -0.158
## 4 Resample01 -0.232 0.0623
## 5 Resample01 -0.0859 0.0173
## 6 Resample01 0.169 0.303I can now compute the RMSE when mtry = 3 and trees = 200:
results_example %>%
group_by(id) %>%
rmse(truth, prediction) %>%
summarise(mean_rmse = mean(.estimate)) %>%
pull## [1] 0.4319164The random forest has already lower RMSE than the linear regression. The goal now is to lower this
RMSE by tuning the mtry and trees hyperparameters. For this, I will use Bayesian Optimization
methods implemented in the {mlrMBO} package.
Bayesian hyperparameter optimization
I will re-use the code from above, and define a function that does everything from pre-processing to returning the metric I want to minimize by tuning the hyperparameters, the RMSE:
tuning <- function(param, validation_data){
mtry <- param[1]
trees <- param[2]
results <- purrr::map2_df(.x = validation_data$splits,
.y = validation_data$id,
~my_rf(mtry = mtry, trees = trees, split = .x, id = .y))
results %>%
group_by(id) %>%
rmse(truth, prediction) %>%
summarise(mean_rmse = mean(.estimate)) %>%
pull
}This is exactly the code from before, but it now returns the RMSE. Let’s try the function with the values from before:
tuning(c(3, 200), validation_data)## [1] 0.4330951Let’s also plot the value of RMSE for mtry = 3 and trees from 200 to 300. This takes some
time, because I need to evaluate this costly function 100 times. If evaluating the function was
cheap, I could have made a 3D plot by varying values of mtry too, but then again if evaluating
the function was cheap, I would run an exhaustive grid search to find the hyperparameters instead of
using Bayesian optimization.
plot_points <- crossing("mtry" = 3, "trees" = seq(200, 300))
plot_data <- plot_points %>%
mutate(value = map_dbl(seq(200, 300), ~tuning(c(3, .), validation_data)))plot_data %>%
ggplot(aes(y = value, x = trees)) +
geom_line(colour = "#82518c") +
theme_blog() +
ggtitle("RMSE for mtry = 3")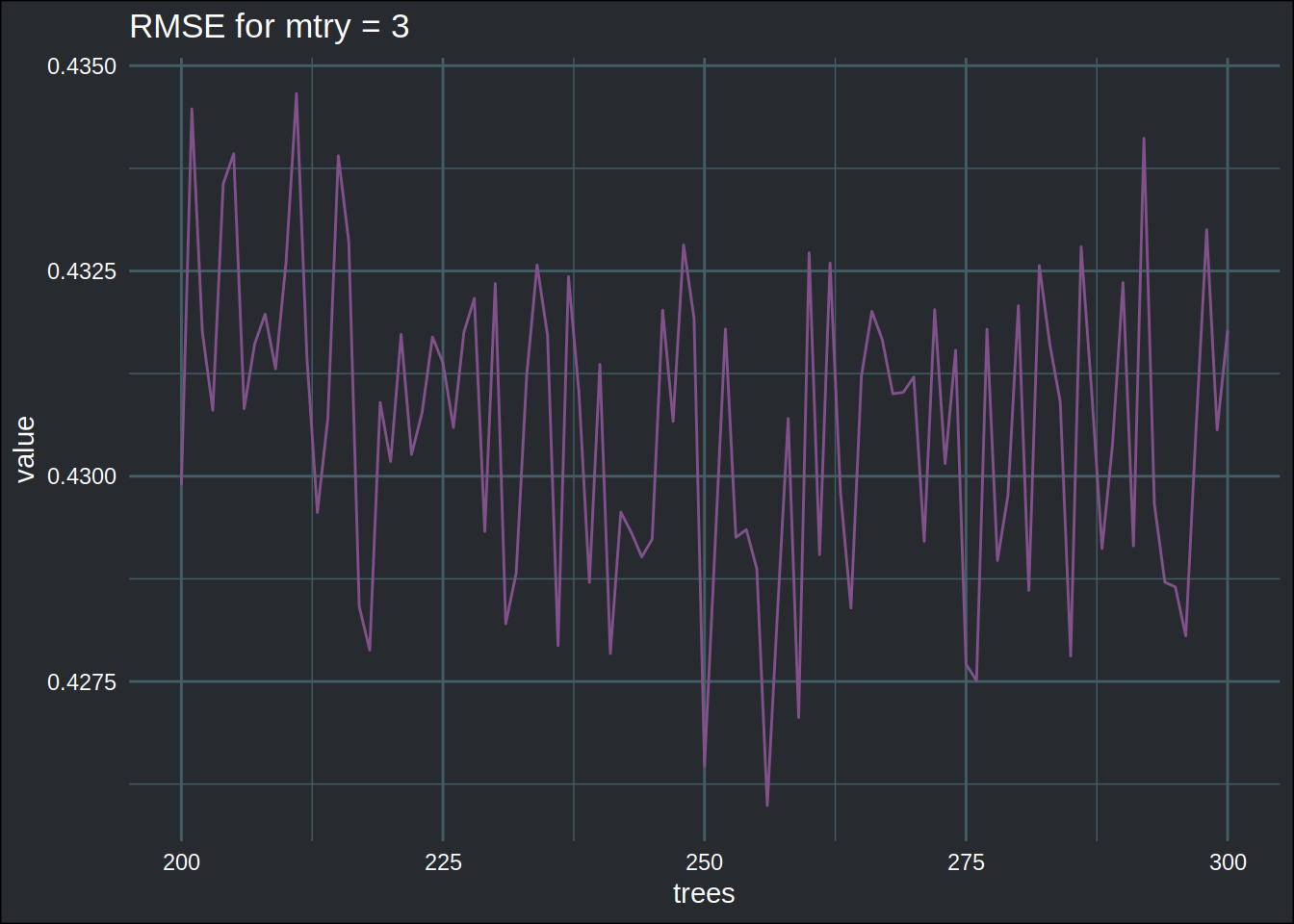
For mtry = 3 the minimum seems to lie around 255. The function to minimize is not smooth at all.
I now follow the code that can be found in the arxiv paper to run the optimization. I think I got the gist of the paper, but I did not understand everything yet. For now, I am still experimenting with the library at the moment, but from what I understand, a simpler model, called the surrogate model, is used to look for promising points and to evaluate the value of the function at these points. This seems somewhat similar (in spirit) to the Indirect Inference method as described in Gourieroux, Monfort, Renault.
Let’s first load the package and create the function to optimize:
library("mlrMBO")fn <- makeSingleObjectiveFunction(name = "tuning",
fn = tuning,
par.set = makeParamSet(makeIntegerParam("x1", lower = 3, upper = 8),
makeIntegerParam("x2", lower = 50, upper = 500)))This function is based on the function I defined before. The parameters to optimize are also
defined as are their bounds. I will look for mtry between the values of 3 and 8, and trees
between 50 and 500.
Now comes the part I didn’t quite get.
# Create initial random Latin Hypercube Design of 10 points
library(lhs)# for randomLHS
des <- generateDesign(n = 5L * 2L, getParamSet(fn), fun = randomLHS)I think this means that these 10 points are the points used to start the whole process. I did not understand why they have to be sampled from a hypercube, but ok. Then I choose the surrogate model, a random forest too, and predict the standard error. Here also, I did not quite get why the standard error can be an option.
# Specify kriging model with standard error estimation
surrogate <- makeLearner("regr.ranger", predict.type = "se", keep.inbag = TRUE)Here I define some options:
# Set general controls
ctrl <- makeMBOControl()
ctrl <- setMBOControlTermination(ctrl, iters = 10L)
ctrl <- setMBOControlInfill(ctrl, crit = makeMBOInfillCritEI())And this is the optimization part:
# Start optimization
result <- mbo(fn, des, surrogate, ctrl, more.args = list("validation_data" = validation_data))result## Recommended parameters:
## x1=6; x2=381
## Objective: y = 0.393
##
## Optimization path
## 10 + 10 entries in total, displaying last 10 (or less):
## x1 x2 y dob eol error.message exec.time ei
## 11 6 370 0.3943479 1 NA <NA> 8.913 -3.134568e-05
## 12 6 362 0.3950402 2 NA <NA> 8.844 -2.987934e-05
## 13 6 373 0.3939587 3 NA <NA> 8.939 -2.259674e-05
## 14 6 394 0.3962875 4 NA <NA> 9.342 -7.427682e-06
## 15 6 368 0.3944954 5 NA <NA> 8.760 -4.121337e-06
## 16 6 378 0.3938796 6 NA <NA> 8.949 -4.503591e-07
## 17 6 381 0.3934176 7 NA <NA> 9.109 -1.141853e-06
## 18 6 380 0.3948077 8 NA <NA> 9.026 -4.718394e-08
## 19 6 381 0.3932636 9 NA <NA> 9.022 -9.801395e-08
## 20 6 383 0.3953004 10 NA <NA> 9.184 -1.579619e-09
## error.model train.time prop.type propose.time se mean
## 11 <NA> 0.014 infill_ei 0.449 0.0010924600 0.3955131
## 12 <NA> 0.012 infill_ei 0.458 0.0007415920 0.3948705
## 13 <NA> 0.012 infill_ei 0.460 0.0006116756 0.3947185
## 14 <NA> 0.012 infill_ei 0.729 0.0003104694 0.3943572
## 15 <NA> 0.023 infill_ei 0.444 0.0003446061 0.3945085
## 16 <NA> 0.013 infill_ei 0.458 0.0002381887 0.3944642
## 17 <NA> 0.013 infill_ei 0.492 0.0002106454 0.3943200
## 18 <NA> 0.013 infill_ei 0.516 0.0002093524 0.3940764
## 19 <NA> 0.014 infill_ei 0.756 0.0002481260 0.3941597
## 20 <NA> 0.013 infill_ei 0.483 0.0001687982 0.3939285So the recommended parameters are 6 for mtry and 381 for trees. The value of the RMSE is lower
than before, and equals 0.393.
Let’s now train the random forest on the training data with this values. First, I pre-process the
training data:
training_rec <- prep(simple_recipe(housing_train), testing = housing_train)
train_data <- bake(training_rec, newdata = housing_train)## Warning: Please use `new_data` instead of `newdata` with `bake`.
## In recipes versions >= 0.1.4, this will cause an error.Let’s now train our final model and predict the prices:
final_model <- rand_forest(mtry = 6, trees = 381) %>%
set_engine("ranger", importance = 'impurity') %>%
fit(price ~ ., data = train_data)
price_predict <- predict(final_model, new_data = select(test_data, -price))Let’s transform the data back and compare the predicted prices to the true ones visually:
cbind(price_predict * sd(housing_train$price) + mean(housing_train$price),
housing_test$price)## .pred housing_test$price
## 1 34.811111 34.7
## 2 20.591304 22.9
## 3 19.463920 18.9
## 4 20.321990 21.7
## 5 19.063132 17.5
## 6 15.969125 14.5
## 7 18.203023 15.6
## 8 17.139943 13.9
## 9 21.393329 24.2
## 10 27.508482 25.0
## 11 24.030162 24.1
## 12 21.222857 21.2
## 13 23.052677 22.2
## 14 20.303233 19.3
## 15 21.134554 21.7
## 16 22.913097 18.5
## 17 20.029506 18.8
## 18 18.045923 16.2
## 19 17.321006 13.3
## 20 18.201785 13.4
## 21 29.928316 32.5
## 22 24.339983 26.4
## 23 45.518316 42.3
## 24 29.551251 26.7
## 25 26.513473 30.1
## 26 42.984738 46.7
## 27 43.513001 48.3
## 28 25.436146 23.3
## 29 21.766247 24.3
## 30 36.328740 36.0
## 31 32.830061 31.0
## 32 38.736098 35.2
## 33 31.573311 32.0
## 34 19.847848 19.4
## 35 23.401032 23.1
## 36 22.000914 19.4
## 37 20.155696 18.7
## 38 21.342003 22.6
## 39 20.846330 19.9
## 40 13.752108 13.8
## 41 12.499064 13.1
## 42 15.019987 16.3
## 43 8.489851 7.2
## 44 7.803981 10.4
## 45 18.629488 20.8
## 46 14.645669 14.3
## 47 15.094423 15.2
## 48 20.470057 17.7
## 49 15.147170 13.3
## 50 15.880035 13.6Let’s now compute the RMSE:
tibble::tibble("truth" = test_data$price,
"prediction" = unlist(price_predict)) %>%
rmse(truth, prediction)## # A tibble: 1 x 3
## .metric .estimator .estimate
## <chr> <chr> <dbl>
## 1 rmse standard 0.327Very nice.
Hope you enjoyed! If you found this blog post useful, you might want to follow me on twitter for blog post updates and buy me an espresso.
