Intermittent demand, Croston and Die Hard

2019/06/12 R

I have recently been confronted to a kind of data set and problem that I was not even aware existed: intermittent demand data. Intermittent demand arises when the demand for a certain good arrives sporadically. Let’s take a look at an example, by analyzing the number of downloads for the {RDieHarder} package:

library(tidyverse)
library(tsintermittent)
library(nnfor)
library(cranlogs)
library(brotools)

rdieharder <- cran_downloads("RDieHarder", from = "2017-01-01")

ggplot(rdieharder) +
  geom_line(aes(y = count, x = date), colour = "#82518c") +
  theme_blog()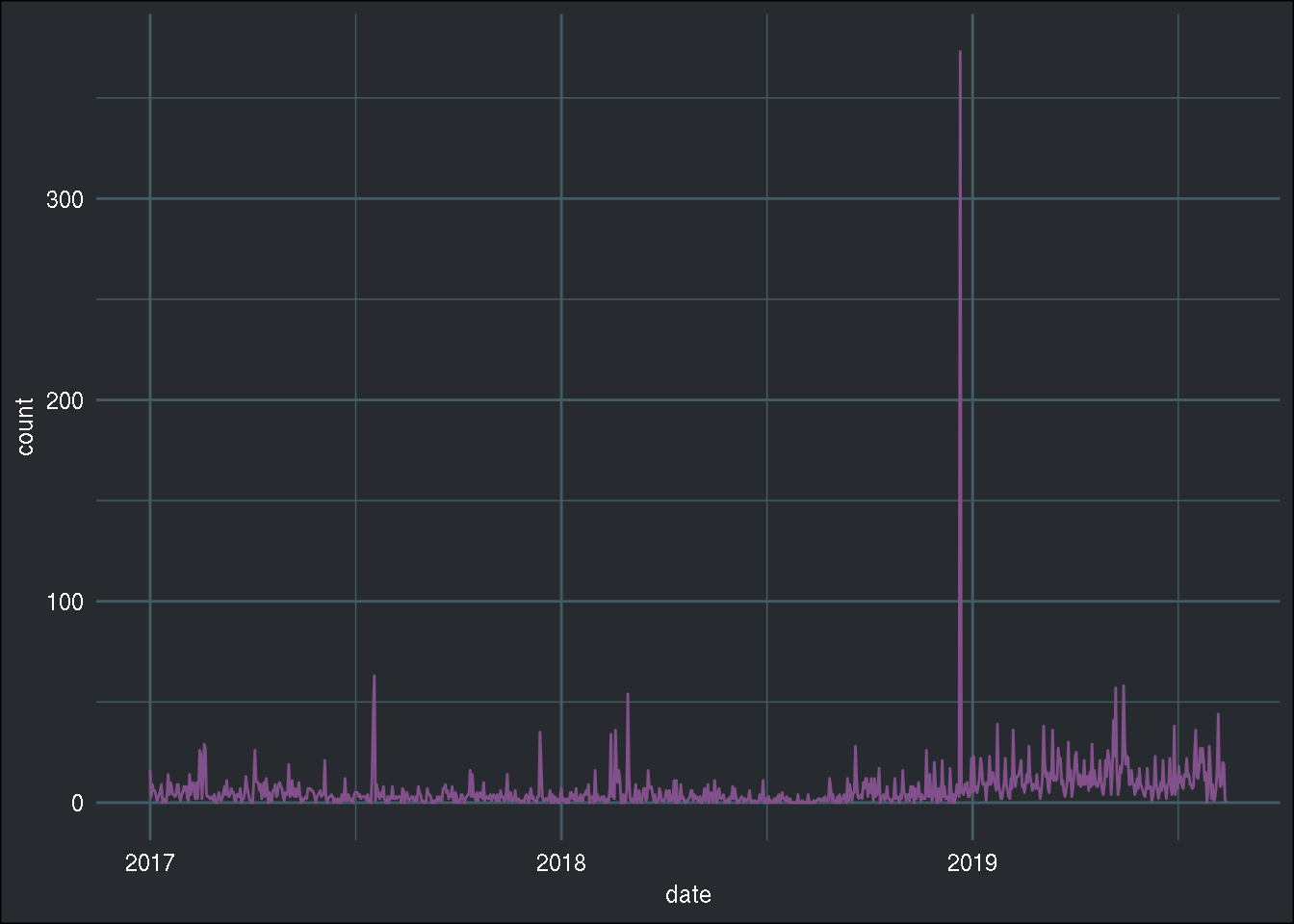

Let’s take a look at just one month of data, because the above plot is not very clear, because of the outlier just before 2019… I wonder now, was that on Christmas day?

rdieharder %>%
  filter(count == max(count))

##         date count    package
## 1 2018-12-21   373 RDieHarder

Not exactly on Christmas day, but almost! Anyways, let’s look at one month of data:

january_2018 <- rdieharder %>%
  filter(between(date, as.Date("2018-01-01"), as.Date("2018-02-01")))

ggplot(january_2018) +
  geom_line(aes(y = count, x = date), colour = "#82518c") +
  theme_blog()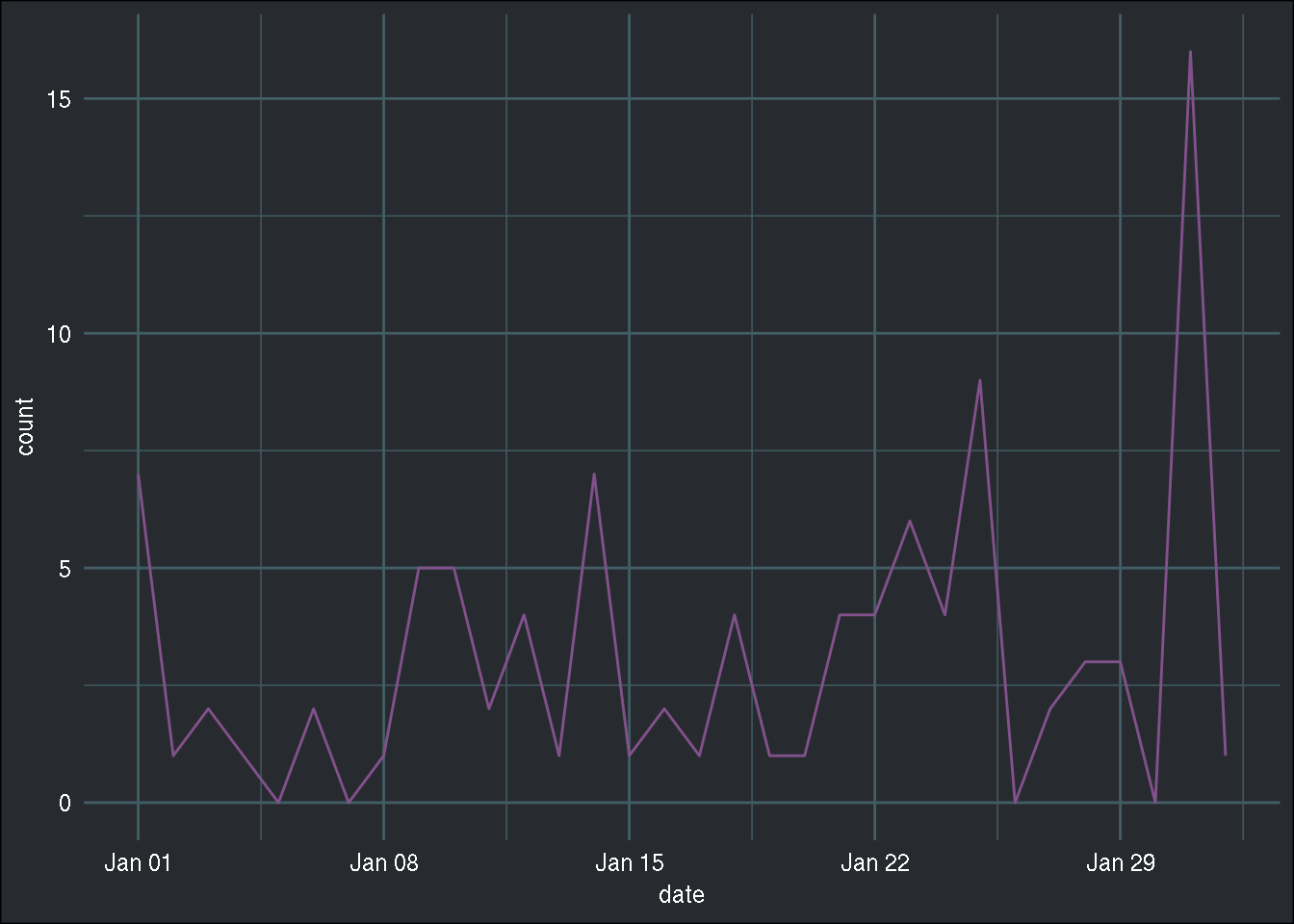

Now, it is clear that this will be tricky to forecast. There is no discernible pattern, no trend, no seasonality… nothing that would make it “easy” for a model to learn how to forecast such data.

This is typical intermittent demand data. Specific methods have been developed to forecast such data, the most well-known being Croston, as detailed in this paper. A function to estimate such models is available in the {tsintermittent} package, written by Nikolaos Kourentzes who also wrote another package, {nnfor}, which uses Neural Networks to forecast time series data. I am going to use both to try to forecast the intermittent demand for the {RDieHarder} package for the year 2019.

Let’s first load these packages:

library(tsintermittent)
library(nnfor)

And as usual, split the data into training and testing sets:

train_data <- rdieharder %>%
  filter(date < as.Date("2019-01-01")) %>%
  pull(count) %>%
  ts()

test_data <- rdieharder %>%
  filter(date >= as.Date("2019-01-01"))

Let’s consider three models; a naive one, which simply uses the mean of the training set as the forecast for all future periods, Croston’s method, and finally a Neural Network from the {nnfor} package:

naive_model <- mean(train_data)

croston_model <- crost(train_data, h = 163)

nn_model <- mlp(train_data, reps = 1, hd.auto.type = "cv")

## Warning in preprocess(y, m, lags, keep, difforder, sel.lag,
## allow.det.season, : No inputs left in the network after pre-selection,
## forcing AR(1).

nn_model_forecast <- forecast(nn_model, h = 163)

The crost() function estimates Croston’s model, and the h argument produces the forecast for the next 163 days. mlp() trains a multilayer perceptron, and the hd.auto.type = "cv" argument means that 5-fold cross-validation will be used to find the best number of hidden nodes. I then obtain the forecast using the forecast() function. As you can read from the Warning message above, the Neural Network was replaced by an auto-regressive model, AR(1), because no inputs were left after pre-selection… I am not exactly sure what that means, but if I remove the big outlier from before, this warning message disappears, and a Neural Network is successfully trained.

In order to rank the models, I follow this paper from Rob J. Hyndman, who wrote a very useful book titled Forecasting: Principles and Practice, and use the Mean Absolute Scaled Error, or MASE. You can also read this shorter pdf which also details how to use MASE to measure the accuracy for intermittent demand. Here is the function:

mase <- function(train_ts, test_ts, outsample_forecast){

  naive_insample_forecast <- stats::lag(train_ts)

  insample_mae <- mean(abs(train_ts - naive_insample_forecast), na.rm = TRUE)
  error_outsample <- test_ts - outsample_forecast

  ase <- error_outsample / insample_mae
  mean(abs(ase), na.rm = TRUE)
}

It is now easy to compute the models’ accuracies:

mase(train_data, test_data$count, naive_model)

## [1] 1.764385

mase(train_data, test_data$count, croston_model$component$c.out[1])

## [1] 1.397611

mase(train_data, test_data$count, nn_model_forecast$mean)

## [1] 1.767357

Croston’s method is the one that performs best from the three. Maybe surprisingly, the naive method performs just as well as the Neural Network! (or rather, the AR(1) model) Let’s also plot the predictions with the true values from the test set:

test_data <- test_data %>%
  mutate(naive_model_forecast = naive_model,
         croston_model_forecast = croston_model$component$c.out[1],
         nn_model_forecast = nn_model_forecast$mean) %>%
  select(-package) %>%
  rename(actual_value = count)


test_data_longer <- test_data %>%
  gather(models, value,
         actual_value, naive_model_forecast, croston_model_forecast, nn_model_forecast)

## Warning: attributes are not identical across measure variables;
## they will be dropped

ggplot(test_data_longer) +
  geom_line(aes(y = value, x = date, colour = models)) +
  theme_blog()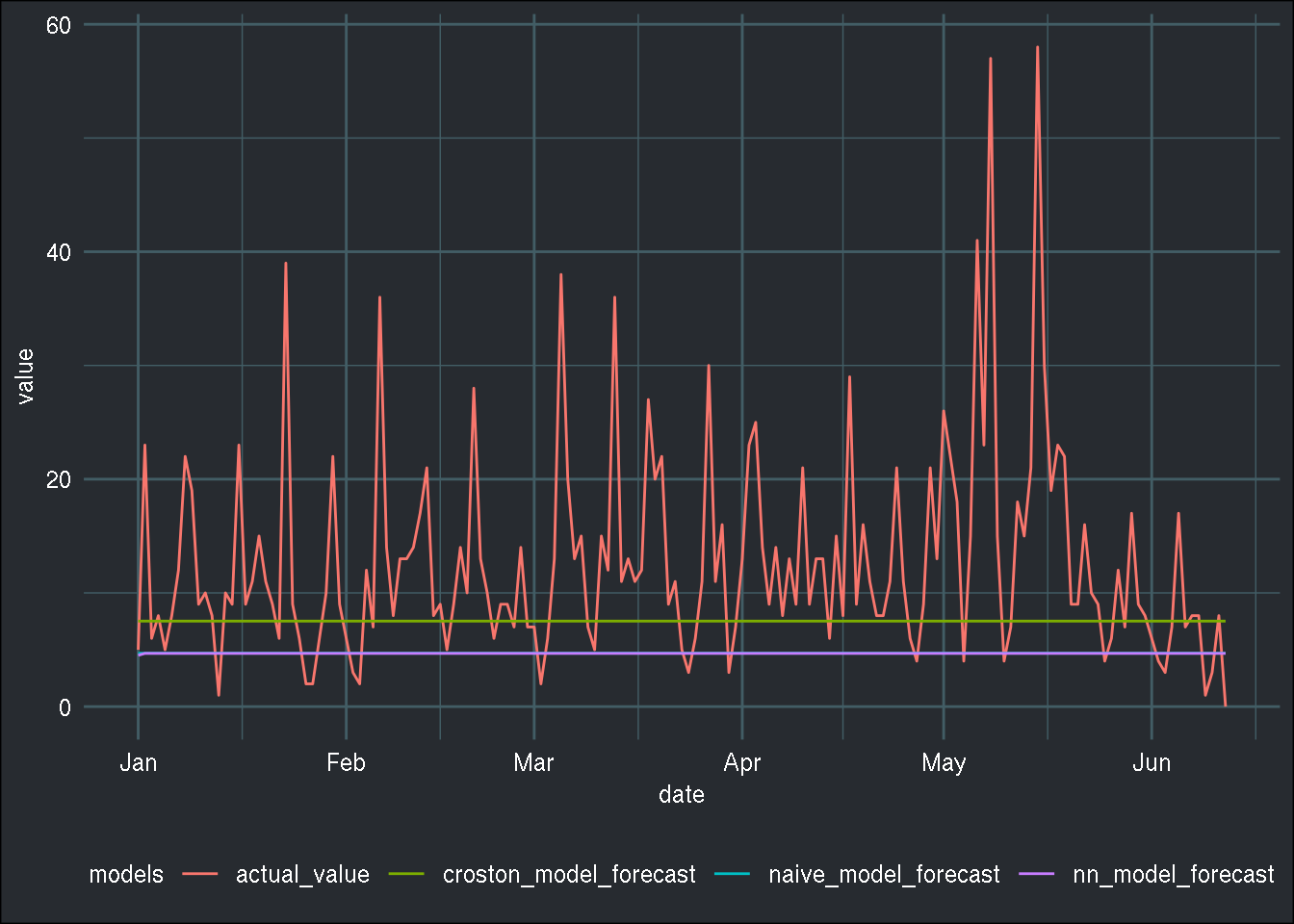

Just to make sure I didn’t make a mistake when writing the mase() function, let’s use the accuracy() function from the {forecast} package and compare the result for the Neural Network:

library(forecast)
accuracy(nn_model_forecast, x = test_data$actual_value)

##                       ME     RMSE      MAE  MPE MAPE      MASE       ACF1
## Training set 0.001929409 14.81196 4.109577  NaN  Inf 0.8437033 0.05425074
## Test set     8.211758227 12.40199 8.635563 -Inf  Inf 1.7673570         NA

The result is the same, so it does seem like the naive method is not that bad, actually! Now, in general, intermittent demand series have a lot of 0 values, which is not really the case here. I still think that the methodology fits to this particular data set.

How else would you have forecast this data? Let me know via twitter!

Hope you enjoyed! If you found this blog post useful, you might want to follow me on twitter for blog post updates and buy me an espresso or paypal.me.

Buy me an Espresso