Dynamic discrete choice models, reinforcement learning and Harold, part 1
RIntroduction
I want to write about an Econometrica paper written in 1987 (jstor link) by John Rust, currently Professor of Economics at Georgetown University, paper which has been on my mind for the past 10 years or so. Why? Because it is a seminal paper in the econometric literature, but it is quite a bizarre one in some aspects. In this paper, John Rust estimates a structural dynamic discrete choice model on real data, and Professor Rust even had to develop his own novel algorithm, which he called NFXP, which stands for Nested Fixed Point algorithm, to estimate the model. Such models hare now part of the toolbox of structural econometricians, because said models are suited to model decision making in a changing environment. How much should you save today for retirement? Should you go to university? If yes, which major should you choose? Should you get a PhD? Should you have kids? How many? With whom? As you see, kind reader, these models are at the center point of what makes life so interesting, and sometimes so scary as well; what will be the impact of our decisions today on future rewards? Some would say that only the Almighty would know, but structural econometricians now know as well, thanks to John Rust.
It is thus completely natural that Professor Rust chose a very important topic and gathered some very important data to illustrate the inner workings of such a complicated, and yet fundamentally important model.
John Rust chose to tell the story of one named Harold Zurcher, superintendent of the Madison, Wisconsin, Metropolitan Bus Company and his monthly decision making process on whether to replace the engine of the buses of the company’s fleet, or not.
And thine ears shall hear a word behind thee, saying, This is the way, walk ye in it, when ye turn to the right hand, and when ye turn to the left., Isaiah 30:21
John Rust’s goal is to write down a model of Harold Zurcher’s behaviour, which he assumes follows an optimal stopping rule: a strategy which specifies whether or not to replace the current bus engine each period as a function of observed and unobserved state variables. But, dear reader, you might wonder, Why model the decisions of Harold Zurcher? Why not any other, more pressing, issue?
Quoting the author gives an answer: Admittedly, few people are likely to take particular interest in Harold Zurcher and bus engine replacement, per se. I focus on a particular individual and a specific capital good because it provides a simple, concrete framework to illustrate two ideas: (i) a “bottom-up” approach for modelling replacement investment and (ii) a “nested fixed point” algorithm for estimating dynamic programming models of discrete choice. And this is what made me absolutely love this paper; I am 100% certain that today, anyone, especially when starting an academic career, could not, and would not, write a paper where one would model something so… non-consequential. And yet, John Rust not only wrote such a paper, his paper is seminal in the literature of structural econometrics. For me, this is one of the best papers I ever read. I read this paper around 2010-ish, and have thought about it on and off since then. I now want to explore the data from his paper, and make you discover it as well.
In this blog post, I will focus on the data of the paper, which you can download in its raw,
original format or tidy format in the github repo I set up
here. In the next blog post, I’ll
discuss the model in greater detail, with a focus on Harold Zurcher’s decisions. I’ll then discuss
the similarities between reinforcement learning (the title of this blog post was not 100% clickbait)
and dynamic discrete stochastic models and use the {ReinforcementLearning} package to try to
estimate the optimal policy. I haven’t tried the package’s function on this paper’s data yet, so
I have no idea if it’s going to work out. We’ll see.
The paper’s data
Harold Zurcher provided monthly data on odometer readings from 162 buses of the Madison Metro fleet to John Rust.
(
I sometimes wonder how this discussion went.
- Hello Mr Zurcher, I’m an economist, my name is John Rust, and I am interested in dynamic discrete choice models and their estimation. I would like to write an empirical paper for a prestigious journal, and would like to know if you would be so kind as to provide me with data for my paper.
- You what?
)
The time period goes from December, 1974 to May, 1985. There are 9 groups of buses, but for a reason that is not explained in the paper only 8 groups of buses are studied. In addition to the monthly odometer readings, there is also the date of a first, or second engine replacement. This is the decision that Harold Zurcher faces each month: should he replace, or not, the engine? This is a simplification from the author; in actuality, Harold Zurcher could also perform a routine maintenance or replace individual components as well. The idea to focus on the third option (complete replacement of the engine) is justified by John Rust as being part of a general “preventive maintenance” strategy. Indeed, if a component of the engine fails at low mileage, it is rather safe to simply replace that component. However, should one component of the engine fail at a much higher mileage, then it is very likely that other components would fail as well in the near future. As such, it is much safer to completely replace the engine, either with a brand new one, or with one freshly rebuilt from the company’s machine shop. John Rust points out that Harold Zurcher assured him that rebuilt engines are every bit as good, if not better, than engines purchased brand new.
Now, to the data itself. The data comes in a format unlike anything I had ever seen before. Let’s take a
look at the head of one single file, for instance a452372.asc (.asc stands for ascii, as far as I know):
4239
2
72
1
76
166100
0
0
0
12
74
140953
142960
145380
148140 Then, on line 138, the data for the second bus of this groups starts:
4240
2
72
1
75
177900
0
0
0
12
74
174402
175116 and so on for each bus of this group. The other files are structured in the same way.
This is quite cryptic, but thankfully, the data is well documented in the manual of the NFXP software that John Rust wrote for this paper (remember the algorithm he wrote to estimate the model? He shared his code with a nice manual, a very good practice that unfortunately is not widespread enough in econometric circles, even to this day). From this manual, we can read that the 11 first lines of the file are some kind of metadata:
| Row | Meaning | Observation |
|---|---|---|
| 1 | bus number | 4239 |
| 2 | month purchased | 2 |
| 3 | year purchased | 72 |
| 4 | month of 1st engine replacement | 1 |
| 5 | year of 1st engine replacement | 76 |
| 6 | odometer at replacement | 166100 |
| 7 | month of 2nd replacement | 0 |
| 8 | year of 2nd replacement | 0 |
| 9 | odometer at replacement | 0 |
| 10 | month odometer data begins | 12 |
| 11 | year odometer data begins | 74 |
| 12 | odometer reading | 140953 |
With this knowledge, the first step is thus to build a tidy data frame. To achieve this, I first load the relevant packages, and read in all the data at once:
library(tidyverse)
library(lubridate)
data_file_path <- Sys.glob("datasets/*.asc")
data_files <- map(data_file_path, read_lines)data_files is a list of 9 elements, where each element is one of the raw data files
(a42372.asc, a452374.asc, ….)
> str(data_files)List of 9
$ : chr [1:2466] " 4239 " " 2 " " 72 " " 1 " ...
$ : chr [1:1370] " 4287 " " 10 " " 74 " " 11 " ...
$ : chr [1:2466] " 5257 " " 5 " " 72 " " 6 " ...
$ : chr [1:1644] " 5275 " " 10 " " 74 " " 9 " ...
$ : chr [1:4736] " 5297 " " 8 " " 75 " " 4 " ...
$ : chr [1:440] " 1334 " " 3 " " 77 " " 0 " ...
$ : chr [1:540] " 4403 " " 5 " " 83 " " 0 " ...
$ : chr [1:240] " 2386 " " 5 " " 81 " " 0 " ...
$ : chr [1:3888] " 4338 " " 3 " " 79 " " 3 " ...to process all this data, I wrote this monster function:
process_bus_data <- function(data_file){
data_file <- as.numeric(data_file)
first_bus <- data_file[1]
second_bus <- first_bus + 1
second_bus_index <- which(data_file == second_bus)
nb_data_points <- second_bus_index - 1
nb_buses <- length(data_file) / nb_data_points
indices <- nb_data_points * seq(1, nb_buses)
indices <- c(0, indices)
sep_data_sets <- map(indices, ~`[`(data_file, (. + 1):(. + nb_data_points) ))
headers_list <- map(sep_data_sets, ~`[`(., 1:11))
header_elements <- c("bus number", "month purchased", "year purchased",
"month of 1st engine replacement", "year of 1st engine replacement",
"odometer at replacement", "month of 2nd replacement",
"year of 2nd replacement", "odometer at replacement",
"month odometer data begins", "year odometer data begins")
create_start_date <- function(one_dataset){
one_dataset <- pull(one_dataset)
month <- one_dataset[10]
year <- paste0("19", one_dataset[11])
month <- ifelse(nchar(month) == 1, paste0("0", month), month)
ymd(paste0(year, "-", month, "-01"))
}
create_first_replacement <- function(one_dataset){
one_dataset <- pull(one_dataset, odometer_reading)
month <- one_dataset[4]
year <- paste0("19", one_dataset[5])
month <- ifelse(nchar(month) == 1, paste0("0", month), month)
ymd(paste0(year, "-", month, "-01"))
}
create_second_replacement <- function(one_dataset){
one_dataset <- pull(one_dataset, odometer_reading)
month <- one_dataset[7]
year <- paste0("19", one_dataset[8])
month <- ifelse(nchar(month) == 1, paste0("0", month), month)
ymd(paste0(year, "-", month, "-01"))
}
get_bus_id <- function(one_dataset){
one_dataset <- pull(one_dataset, odometer_reading)
one_dataset[1]
}
named_headers <- map(headers_list, ~set_names(., header_elements))
raw_data <- map(sep_data_sets, ~tibble("odometer_reading" = .))
raw_data <- map(raw_data, ~mutate(., "date" = create_start_date(.)))
raw_data <- map(raw_data, ~mutate(., "first_replacement_date" = create_first_replacement(.)))
raw_data <- map(raw_data, ~mutate(., "second_replacement_date" = create_second_replacement(.)))
raw_data <- map(raw_data, ~mutate(., "bus_id" = get_bus_id(.)))
raw_data <- map(raw_data, ~slice(., -c(1:11)))
fill_dates <- function(vector){
for(i in 2:length(vector)){
vector[i] <- add_with_rollback(vector[i-1], months(1))
# the line below can be uncommented to skip the 2 months of strike in 1980
#vector[i] <- if_else(vector[i] == ymd("1980-07-01"), add_with_rollback(vector[i], months(2)),
# vector[i])
}
vector
}
raw_data <- raw_data %>%
map(~mutate(., date = fill_dates(date)))
raw_data <- map(raw_data, ~mutate(., "replacement_1" = if_else(date == first_replacement_date, 1, 0, 0)))
raw_data <- map(raw_data, ~mutate(., "replacement_2" = if_else(date == second_replacement_date, 1, 0, 0)))
raw_data <- map(raw_data, ~mutate(., replacement = replacement_1 + replacement_2))
raw_data <- map(raw_data, ~select(., bus_id, date, odometer_reading, replacement,
-replacement_1, -replacement_2, -first_replacement_date, -second_replacement_date))
return(raw_data)
}Now, as usual, I didn’t write this in one go. First, I experimented bits and pieces of code on one single dataset, and then only started putting these pieces together into this big function.
I won’t go through this function line by line, because it would take me ages. I think there are two majors things to understand in this function:
- first identify the start of a particular bus’s data;
- second this function uses some intermediary
{purrr}magic.
So first step, identify the start of the monthly odometer reading for one bus. For the first bus this is quite simple, as it is simply the start of the file. But when does the data for the second bus start? Thankfully, buses’ ids are numbers, and they’re in incrementing order in the data. I use this to get the index of the second bus, and compute the number of rows between the id of the first and second bus, which gives me the number of months of odometer readings for the first bus.
data_file <- as.numeric(data_file)
first_bus <- data_file[1]
second_bus <- first_bus + 1
second_bus_index <- which(data_file == second_bus)
nb_data_points <- second_bus_index - 1Then, I get the number of buses in the data, and create a vector with all the indices of the buses’ ids:
nb_buses <- length(data_file) / nb_data_points
indices <- nb_data_points * seq(1, nb_buses)
indices <- c(0, indices)
sep_data_sets <- map(indices, ~`[`(data_file, (. + 1):(. + nb_data_points) ))I end up with a list of lists, sep_data_sets.
The first element of my list is now a list, with the data from the
a452372.asc file, where each element is the data for a single bus.
For instance, here is the first element of sep_data_sets:
str(sep_data_sets[[1]])
List of 19
$ : num [1:137] 4239 2 72 1 76 ...
$ : num [1:137] 4240 2 72 1 75 ...
$ : num [1:137] 4241 2 72 5 75 ...
$ : num [1:137] 4242 2 72 2 76 ...
$ : num [1:137] 4243 2 72 4 76 ...
$ : num [1:137] 4244 2 72 3 78 ...
$ : num [1:137] 4245 2 72 1 75 ...
$ : num [1:137] 4246 2 72 3 75 ...
$ : num [1:137] 4247 2 72 9 80 ...
$ : num [1:137] 4248 2 72 2 75 ...
$ : num [1:137] 4249 2 72 7 75 ...
$ : num [1:137] 4250 2 72 4 80 ...
$ : num [1:137] 4251 2 72 1 79 ...
$ : num [1:137] 4252 2 72 5 76 ...
$ : num [1:137] 4253 2 72 1 77 ...
$ : num [1:137] 4254 2 72 3 76 ...
$ : num [1:137] 4255 2 72 1 76 ...
$ : num [1:137] 4256 2 72 9 77 ...
$ : num [1:137] NA NA NA NA NA NA NA NA NA NA ...So there are 18 buses in the first group of data (the last line full of NA’s is due to the fact that I messed up my indices vector, I’ll simply remove these at the end).
That’s the first step. The second step, is to make use of this list structure to apply some
cleaning functions to each dataset using {purrr}. I explain the approach in my ebook, which you
can read for free
here.
The idea is to use a function that would work on a single element of your list, and then mapping
this over all the elements of the list. For instance, remember that the 11 first elements of
the data are some kind of header? To extract those for one single vector of observations, one
would use:
my_vector[1:11]or, equivalently:
`[`(my_vector, 1:11)Well, when faced with a list of vectors, one maps this function over the whole list using map():
map(my_list_of_vectors, `[`(1:11))This is the logic of this big process_bus_data() function. If something’s not clear after you study
it, drop me an email or tweet.
Anyways, now that I cleaned the data, here’s how it looks:
all_buses <- read_csv("https://raw.githubusercontent.com/b-rodrigues/rust/ee15fb87fc4ba5db28d055c97a898b328725f53c/datasets/processed_data/all_buses.csv")## Parsed with column specification:
## cols(
## bus_id = col_double(),
## date = col_date(format = ""),
## odometer_reading = col_double(),
## replacement = col_double(),
## bus_family = col_character()
## )head(all_buses)## # A tibble: 6 x 5
## bus_id date odometer_reading replacement bus_family
## <dbl> <date> <dbl> <dbl> <chr>
## 1 4239 1974-12-01 140953 0 a452372
## 2 4239 1975-01-01 142960 0 a452372
## 3 4239 1975-02-01 145380 0 a452372
## 4 4239 1975-03-01 148140 0 a452372
## 5 4239 1975-04-01 150921 0 a452372
## 6 4239 1975-05-01 153839 0 a452372This tidy data frame now has the bus id, the odometer readings with the right date, and whether a replacement occurred at that date. I said the right date, but in the original documentation of the data, John Rust mentions a two month strike in July and August 1980, and he removed these points from the data since the odometer readings where the same. I did not skip July and August when I created the dates, even though I have added the code to do it in the function above, because it does not matter.
I have 166 in my sample, while John Rust writes in the paper that his sample contains 162. I do not know why I have 4 more buses.
Let’s try to reproduce Table 2a of the paper (mileage at replacement):
all_buses %>%
group_by(bus_id) %>%
filter(replacement == 1) %>%
group_by(bus_family) %>%
summarise_at(.vars = vars(odometer_reading),
.funs = list(~max(.), ~min(.), ~mean(.), ~sd(.)))## # A tibble: 6 x 5
## bus_family max min mean sd
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 a452372 334393 130810 193175. 53533.
## 2 a452374 237287 82370 151495 61246.
## 3 a530872 413132 170508 278292. 78529.
## 4 a530874 325336 117986 247119 60818.
## 5 a530875 388254 120709 263405. 64556.
## 6 t8h203 273369 125643 200685. 37120.I find different slightly results, for instance, for bus family t8h203 I find an average of
200’685 miles, while the original author found 199’733. This difference comes very likely from
the fact that the author probably uses the value from the header, “odometer at replacement”, at
position 6, while I use the value of the odometer at that month, which is always slightly different.
Let’s try to reproduce Table 2b, as well, mileage for buses who did not have a replacement:
all_buses %>%
group_by(bus_id) %>%
filter(all(replacement == 0)) %>%
group_by(bus_family) %>%
summarise_at(.vars = vars(odometer_reading),
.funs = list(~max(.), ~min(.), ~mean(.), ~sd(.)))## # A tibble: 7 x 5
## bus_family max min mean sd
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 a452374 299040 4249 156135. 81992.
## 2 a530874 326843 13065 197547. 86692.
## 3 a530875 352450 129 188193. 104453.
## 4 d309 65045 294 30643. 17063.
## 5 g870 120151 483 49582. 32353.
## 6 rt50 161748 1743 77506. 44674.
## 7 t8h203 280802 2950 127964. 72300.Here I find exactly the same values as the author. To finish this quite long blog post, let’s now plot the data:
ggplot(all_buses) +
geom_line(aes(y = odometer_reading, x = date, group = bus_id, col = bus_family)) +
labs(title = "Odometer readings") +
brotools::theme_blog()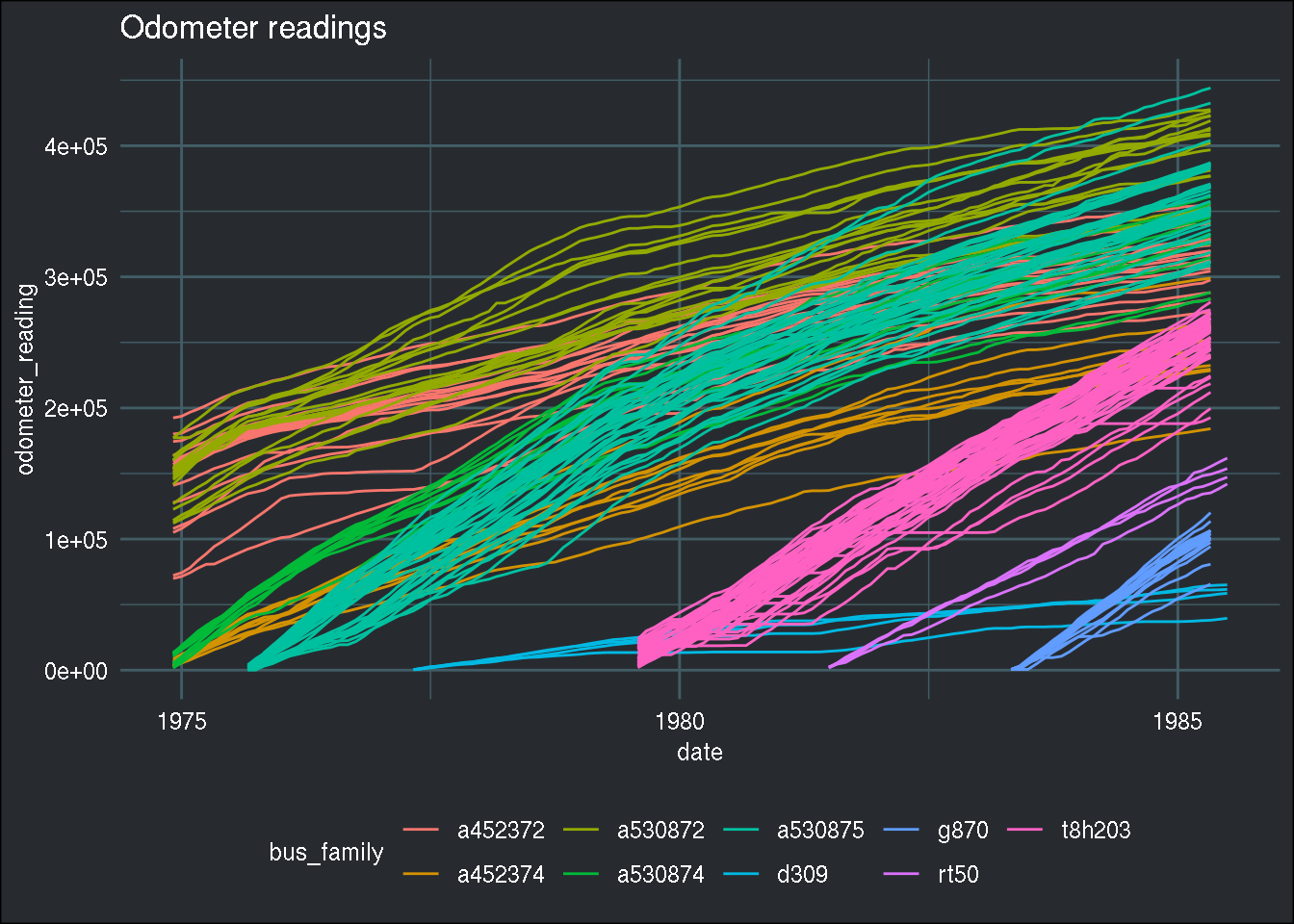
Let’s add some dots to mark the points in time where replacements happened:
ggplot(all_buses) +
geom_line(aes(y = odometer_reading, x = date, group = bus_id, col = bus_family)) +
geom_point(aes(y = ifelse(odometer_reading*replacement == 0, NA, odometer_reading*replacement),
x = date), col = "red") +
labs(title = "Odometer readings and points in time where engine replacement occurred") +
brotools::theme_blog()## Warning: Removed 15840 rows containing missing values (geom_point).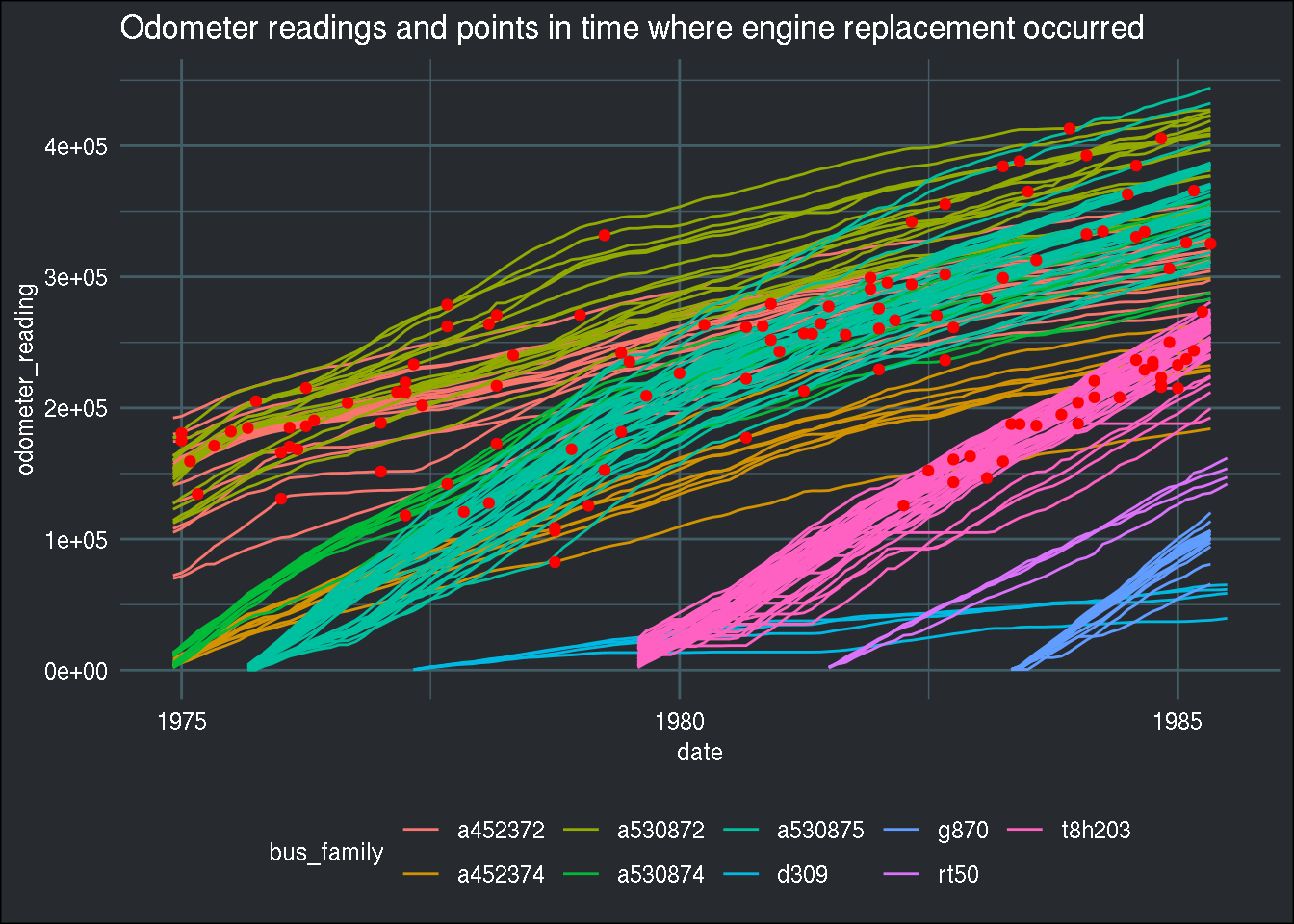
Let’s create a graph for each bus family:
ggplot(all_buses) +
geom_line(aes(y = odometer_reading, x = date, group = bus_id), col = "#82518c") +
geom_point(aes(y = ifelse(odometer_reading*replacement == 0, NA, odometer_reading*replacement),
x = date), col = "red") +
facet_wrap(~bus_family) +
labs(title = "Odometer readings and points in time where engine replacement occurred") +
brotools::theme_blog()## Warning: Removed 15840 rows containing missing values (geom_point).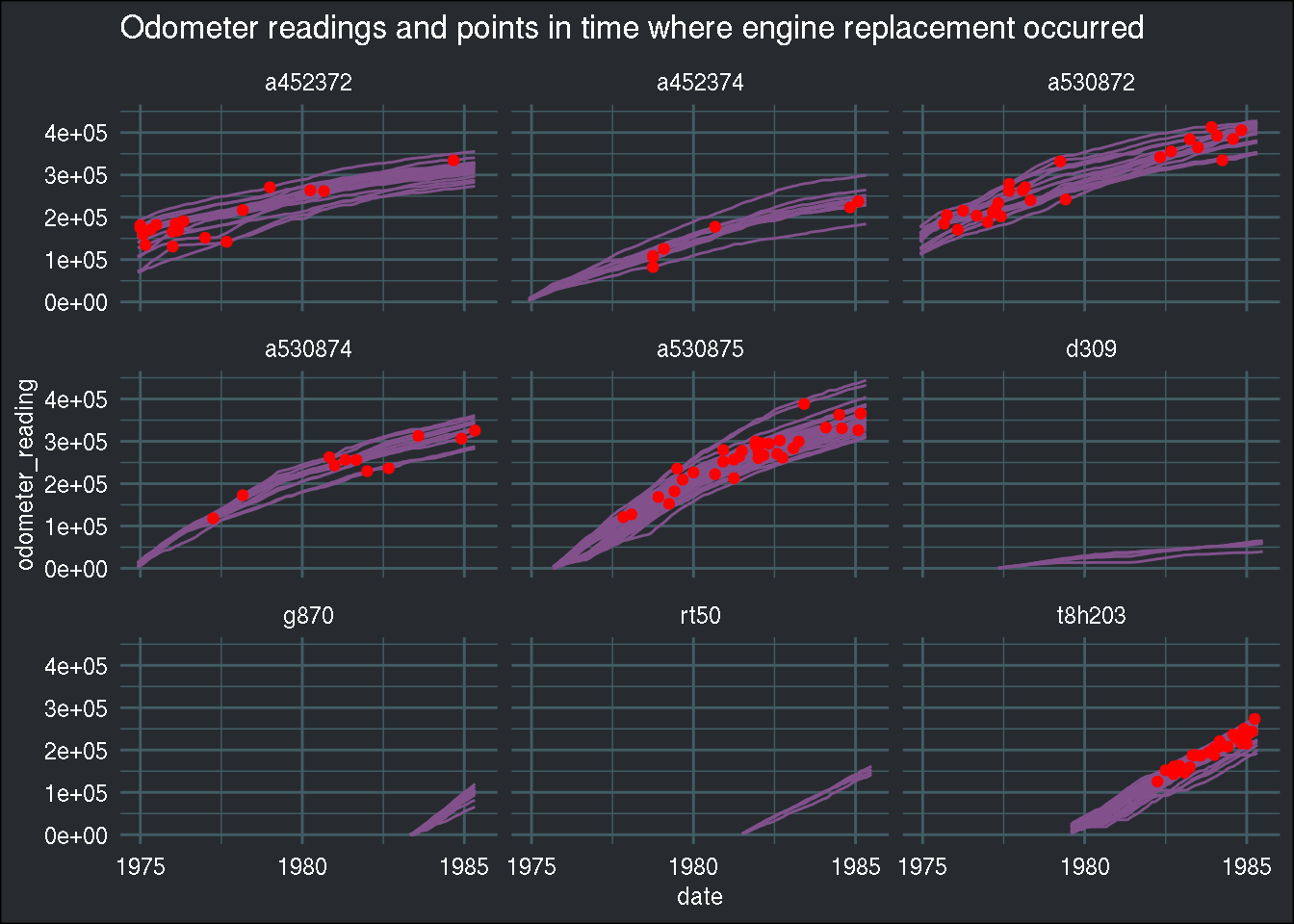
In the next blog post, I’ll explore how recent reinforcement learning methods might help us get the optimal policy from the data!
Hope you enjoyed! If you found this blog post useful, you might want to follow me on twitter for blog post updates and buy me an espresso or paypal.me, or buy my ebook on Leanpub.

