The quest for fast(er?) row-oriented workflows
RPart 2 of this blog post is available here
The past few weeks I have been exploring the speed of R. It started with this video in which I explained that R is not necessarily slower than any other interpreted language, as long as you’re using the built-in, optimized functions. However should you write your own implementation of an algorithm, especially if that algorithm requires the use of one (or more…) loops, it’ll run slowly. As I’ve also mentioned in two other videos, here and here there are many ways to avoid loops, and you should do so if possible.
To continue exploring this is in more detail, I’ve written two very basic implementations of a
genetic algorithm. The first version uses only {tidyverse} functions and the other only base R
functions. My intuition was that base would be faster, but the code would likely be less
“readable” (I discuss this code in greater detail in a series of videos, you can watch
part 1 and part 2
if you’re interested in the nitty-gritty details). Code readability is quite subjective, but I think
that there are some general “truths” regarding it, namely that it seems to often be that case that
fast code is code that is “less” readable, and vice-versa. This blog post explores this trade-off
in the context of row-oriented workflows.
Once I was done writing the two versions of the genetic algorithm for the video
(a {tidyverse} one and a base one), I profiled the code
and realised that, yes base was much much faster, but also that the reason the {tidyverse} version
was running so slowly was because of one single row-based operation. Trying to replace this row-based
operation, but remaining inside the {tidyverse} made for an interesting challenge. I will
explain what I did in this blog post, so first let’s set up the example:
library(tidyverse)
library(brotools)Let’s first generate some data. For this, I’m going to use a function I wrote for my genetic algorithm. I won’t explain how it works, so if you’re curious, you can watch the videos I mention in the introduction where this is all explained in detail:
init_pop <- function(objective_function, pop_size = 100, upper_bound = 1, lower_bound = 0){
parameters <- formals(objective_function)[[1]] %>%
eval
purrr::rerun(length(parameters), runif(n = pop_size,
min = lower_bound,
max = upper_bound)) %>%
dplyr::bind_cols() %>%
janitor::clean_names()
}This function takes another function, the objective function to be optimized, as an argument, and checks how many parameters this objective functions has, and generates a population of random solutions (if you don’t understand what this all means don’t worry. What matters is that this generates a random dataset whith as many columns as the objective function has arguments).
The next function is my objective function:
my_function <- function(x = c(0, 0, 0, 0, 0, 0)){
x1 <- x[1]
x2 <- x[2]
x3 <- x[3]
x4 <- x[4]
x5 <- x[5]
x6 <- x[6]
-(x1**2 + x2 - 11)**2 - (x1 + x2**2 - 7)**2 - (x3**3 + x4 - 11)**2 - (x5 + x6**2 - 7)**2
}(This is not the same as in the videos, which only has two arguments.)
Let’s generate some data:
dataset <- init_pop(my_function) %>%
as.data.frame()head(dataset)## x1 x2 x3 x4 x5 x6
## 1 0.3045714 0.1436057 0.003754794 0.9144551 0.53070392 0.6127125
## 2 0.3155244 0.8890011 0.556325257 0.5688512 0.02928638 0.5626903
## 3 0.8363487 0.6361570 0.667718047 0.4704217 0.10547741 0.5278469
## 4 0.8207208 0.1286540 0.189744816 0.3309174 0.76311349 0.7019268
## 5 0.7244419 0.1284358 0.235967085 0.8444759 0.38697023 0.9818212
## 6 0.2882561 0.9702481 0.983408531 0.1510577 0.84844059 0.7678110Now, on the actual problem: I need to add another column, with the value of my_function(),
evaluated on a per row basis. As an example, for the first row, this would be the result of:
my_function(dataset[1, ])## x1
## 1 -299.2624Many people would probably solve this using a for loop, so let’s write a function to do just that (benchmarking will make it easier if the code is inside a function):
run_loop <- function(dataset, my_function = my_function){
dataset$score <- 0
for(i in seq(1, nrow(dataset))){
dataset$score[i] <- my_function(dataset[i, ])
}
dataset
}
run_loop(dataset, my_function = my_function) %>%
head## x1 x2 x3 x4 x5 x6 score
## 1 0.3045714 0.1436057 0.003754794 0.9144551 0.53070392 0.6127125 -299.2624
## 2 0.3155244 0.8890011 0.556325257 0.5688512 0.02928638 0.5626903 -284.4934
## 3 0.8363487 0.6361570 0.667718047 0.4704217 0.10547741 0.5278469 -275.027
## 4 0.8207208 0.1286540 0.189744816 0.3309174 0.76311349 0.7019268 -288.6529
## 5 0.7244419 0.1284358 0.235967085 0.8444759 0.38697023 0.9818212 -281.0109
## 6 0.2882561 0.9702481 0.983408531 0.1510577 0.84844059 0.7678110 -261.1376The advantage of loops is that you don’t need to really know a lot about R to get it done; if you’ve learned some programming language some time during your studies, you learned about for loops. But they’re generally slower than other methods and error-prone (typos for example, or if you’re looping over several indeces, it can get quite complex…). And they’re, in my humble opinion, not always very easy to understand. This is not the case here, because it is quite a simple example, but often, it can get quite confusing to understand what is going on.
So what would be a more “R-specific” way of doing it (specific in the sense that it is not a
universal solution like a for-loop), and which avoids using a loop?
apply() would here be the best candidate:
apply(dataset, MARGIN = 1, FUN = my_function)## [1] -299.2624 -284.4934 -275.0270 -288.6529 -281.0109 -261.1376 -293.7069
## [8] -264.7833 -270.6977 -258.5214 -299.6117 -275.8491 -306.8555 -284.7410
## [15] -298.6167 -299.2872 -294.9865 -264.5808 -272.8924 -289.5542 -306.3602
## [22] -293.4290 -305.9189 -276.9193 -286.1938 -291.7530 -289.3610 -290.8470
## [29] -303.5995 -261.4664 -280.6596 -287.2716 -282.6859 -293.5323 -304.2287
## [36] -286.9913 -258.3523 -275.9231 -304.3919 -250.9952 -286.7151 -255.0904
## [43] -312.2109 -254.5034 -255.9284 -287.8201 -285.9853 -290.8199 -309.0086
## [50] -311.4288 -271.1889 -299.3821 -290.1711 -281.0423 -294.1406 -275.8203
## [57] -274.1912 -257.7994 -308.3508 -271.5294 -293.3045 -296.9122 -277.8800
## [64] -296.9870 -314.1470 -270.0065 -288.3262 -252.3774 -263.9164 -286.9263
## [71] -302.5980 -281.0731 -269.0754 -301.6335 -294.3153 -268.4932 -263.6926
## [78] -306.9723 -271.8796 -292.6175 -294.0995 -303.4289 -280.5853 -277.6487
## [85] -262.2476 -310.0217 -281.7774 -292.7697 -295.8509 -269.0880 -253.2403
## [92] -279.8632 -293.0479 -258.1470 -303.6226 -306.4314 -293.4026 -275.8508
## [99] -269.6470 -285.0784Appending this to a dataframe can be done within a mutate() call (here again I’m encapsulating
this inside a function, for benchmarking purposes):
run_apply <- function(dataset, my_function = my_function){
dataset %>%
mutate(score = apply(., MARGIN = 1, my_function))
}
run_apply(dataset, my_function = my_function) %>%
head()## x1 x2 x3 x4 x5 x6 score
## 1 0.3045714 0.1436057 0.003754794 0.9144551 0.53070392 0.6127125 -299.2624
## 2 0.3155244 0.8890011 0.556325257 0.5688512 0.02928638 0.5626903 -284.4934
## 3 0.8363487 0.6361570 0.667718047 0.4704217 0.10547741 0.5278469 -275.0270
## 4 0.8207208 0.1286540 0.189744816 0.3309174 0.76311349 0.7019268 -288.6529
## 5 0.7244419 0.1284358 0.235967085 0.8444759 0.38697023 0.9818212 -281.0109
## 6 0.2882561 0.9702481 0.983408531 0.1510577 0.84844059 0.7678110 -261.1376MARGIN = 1 means that the function is applied on the rows, whereas MARGIN = 2 would apply the
function over columns.
In terms of readability, I think that this is maybe a bit less readable than the for-loop, just
because for-loops as very very ubiquitous. But it’s super simple once you understand how apply() works.
Now, what would be a {tidyverse}-only approach? And why would you want to do a {tidyverse}-only
approach anyways? Generally, I would argue that scripts written using {tidyverse} functions and style are
easier to read. For example, I tweeted this code snippet some time ago:
blogdown::shortcode("tweet",
"1431718740341764099"
)I don't see how one could prefer base #RStats
— Bruno Rodrigues (@brodriguesco@fosstodon.org) (@brodriguesco) August 28, 2021
but then again, there's people out there who like licorice candies... pic.twitter.com/bwW74SRDrN
and in my opinion the example in my tweet shows clearly that the {tidyverse} code is more easily
understood and readable. Of course, some people disagree…
However, in this case here, I’m not sure that a {tidyverse} approach would be more readable.
The solution using apply() seems to me to be quite good. Let’s see how the {tidyverse} approach,
which leverages rowwise(), looks like:
run_rowwise <- function(dataset, my_function = my_function){
dataset %>%
rowwise() %>%
mutate(score = my_function(c_across(everything()))) %>%
ungroup()
}
run_rowwise(dataset, my_function = my_function) %>%
head()## # A tibble: 6 × 7
## x1 x2 x3 x4 x5 x6 score
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 0.305 0.144 0.00375 0.914 0.531 0.613 -299.
## 2 0.316 0.889 0.556 0.569 0.0293 0.563 -284.
## 3 0.836 0.636 0.668 0.470 0.105 0.528 -275.
## 4 0.821 0.129 0.190 0.331 0.763 0.702 -289.
## 5 0.724 0.128 0.236 0.844 0.387 0.982 -281.
## 6 0.288 0.970 0.983 0.151 0.848 0.768 -261.This runs, but much, much, more slower than with apply() (but faster than a for-loop, as we
shall see) . Plus, it does look much, much
more complicated than the simple apply() version! So why do it like this? You even need several
functions
- rowwise(), c_across() and everything() - to make it work! So why? Well, there is one use
case in which this approach enables you to do something that I don’t think is possible (or at least
easily possible) with apply() which is applying the function, but only over certain columns. For example,
if you want to apply the function only over the columns which names all start with the letter “c”,
you could write something like this:
mtcars %>%
rowwise() %>%
mutate(score = mean(c_across(starts_with("c")))) %>%
ungroup()## # A tibble: 32 × 12
## mpg cyl disp hp drat wt qsec vs am gear carb score
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 21 6 160 110 3.9 2.62 16.5 0 1 4 4 5
## 2 21 6 160 110 3.9 2.88 17.0 0 1 4 4 5
## 3 22.8 4 108 93 3.85 2.32 18.6 1 1 4 1 2.5
## 4 21.4 6 258 110 3.08 3.22 19.4 1 0 3 1 3.5
## 5 18.7 8 360 175 3.15 3.44 17.0 0 0 3 2 5
## 6 18.1 6 225 105 2.76 3.46 20.2 1 0 3 1 3.5
## 7 14.3 8 360 245 3.21 3.57 15.8 0 0 3 4 6
## 8 24.4 4 147. 62 3.69 3.19 20 1 0 4 2 3
## 9 22.8 4 141. 95 3.92 3.15 22.9 1 0 4 2 3
## 10 19.2 6 168. 123 3.92 3.44 18.3 1 0 4 4 5
## # … with 22 more rowsNow this is not needed here, so apply() clearly wins in terms readability (and speed as well).
But in cases like the above, where you need to compute only over several columns, I think that the
{tidyverse} version not only is very readible, but actually offers a solution to the problem. I’m
not quite sure you could solve this easily with base, but please prove me wrong.
In any case, there’s another way to approach our original problem using {tidyverse} functions,
but we still need the help of a base function.
The next approach uses the fact that map() needs both a list and a function as an input. As a
refresher, here’s how map works:
# We have a list
my_list <- list("a" = 2,
"b" = 4)
# and we have a function, say sqrt, which we want to apply to each element of this list
map(my_list, sqrt)## $a
## [1] 1.414214
##
## $b
## [1] 2So what we need is a way to mimick the basic approach which works on one “element” (in this case,
a row of the dataframe), and extend that idea to a “list of rows”.
Now, the issue is that a dataframe is actually a list of columns, not rows. So if you’re using
map() over a dataframe, you will be looping over the columns, not the rows, as in the
example below:
# This applies the function class() to each colum of mtcars
mtcars %>%
map(class)## $mpg
## [1] "numeric"
##
## $cyl
## [1] "numeric"
##
## $disp
## [1] "numeric"
##
## $hp
## [1] "numeric"
##
## $drat
## [1] "numeric"
##
## $wt
## [1] "numeric"
##
## $qsec
## [1] "numeric"
##
## $vs
## [1] "numeric"
##
## $am
## [1] "numeric"
##
## $gear
## [1] "numeric"
##
## $carb
## [1] "numeric"Now the question becomes; is there a way to turn a dataframe, which is a list of columns,
into a list of rows? Yes, there is, using asplit():
asplit(mtcars, MARGIN = 1) %>%
head()## $`Mazda RX4`
## mpg cyl disp hp drat wt qsec vs am gear carb
## 21.00 6.00 160.00 110.00 3.90 2.62 16.46 0.00 1.00 4.00 4.00
##
## $`Mazda RX4 Wag`
## mpg cyl disp hp drat wt qsec vs am gear
## 21.000 6.000 160.000 110.000 3.900 2.875 17.020 0.000 1.000 4.000
## carb
## 4.000
##
## $`Datsun 710`
## mpg cyl disp hp drat wt qsec vs am gear carb
## 22.80 4.00 108.00 93.00 3.85 2.32 18.61 1.00 1.00 4.00 1.00
##
## $`Hornet 4 Drive`
## mpg cyl disp hp drat wt qsec vs am gear
## 21.400 6.000 258.000 110.000 3.080 3.215 19.440 1.000 0.000 3.000
## carb
## 1.000
##
## $`Hornet Sportabout`
## mpg cyl disp hp drat wt qsec vs am gear carb
## 18.70 8.00 360.00 175.00 3.15 3.44 17.02 0.00 0.00 3.00 2.00
##
## $Valiant
## mpg cyl disp hp drat wt qsec vs am gear carb
## 18.10 6.00 225.00 105.00 2.76 3.46 20.22 1.00 0.00 3.00 1.00asplit() splits a dataframe along rows (with the MARGIN argument set to 1) or along columns
(with MARGIN = 2). As you can see with the code above, the mtcars dataset is now a list of
rows. Each element of this list is a single vector of values.
Now that my dataframe is now a list of rows, well, I can simply use map() to apply any function
over its rows:
run_map <- function(dataset, my_function = my_function){
dataset %>%
mutate(score = map_dbl(asplit(., 1), .f = my_function))
}
run_map(dataset, my_function = my_function) %>%
head()## x1 x2 x3 x4 x5 x6 score
## 1 0.3045714 0.1436057 0.003754794 0.9144551 0.53070392 0.6127125 -299.2624
## 2 0.3155244 0.8890011 0.556325257 0.5688512 0.02928638 0.5626903 -284.4934
## 3 0.8363487 0.6361570 0.667718047 0.4704217 0.10547741 0.5278469 -275.0270
## 4 0.8207208 0.1286540 0.189744816 0.3309174 0.76311349 0.7019268 -288.6529
## 5 0.7244419 0.1284358 0.235967085 0.8444759 0.38697023 0.9818212 -281.0109
## 6 0.2882561 0.9702481 0.983408531 0.1510577 0.84844059 0.7678110 -261.1376So we now have 4 approaches to solve the issue:
run_loop(): uses a for-looprun_apply(): usesapply(), a base R functionrun_rowwise(): a “pure”{tidyverse}approachrun_map(): a cross between a{tidyverse}and a base approach
Let’s set up a function to run some benchmarks and see which runs faster. I’ll create a list of increasingly large data frames over which I’ll run all the above functions:
list_datasets <- map(seq(2, 5), ~init_pop(objective_function = my_function,
pop_size = `^`(10, .x)))The function below will run the benchmarks over all the data frames:
run_benchmarks <- function(dataset, times = 5){
microbenchmark::microbenchmark(
run_loop(dataset, my_function = my_function),
run_apply(dataset, my_function = my_function),
run_rowwise(dataset, my_function = my_function),
run_map(dataset, my_function = my_function),
times = times,
unit = "s"
)
}I’ll run this in parallel using {furrr}:
library(furrr)
plan(multisession, workers = 2)
benchmark_results <- future_map(list_datasets, run_benchmarks)Let’s take a look at the results:
benchmark_data <- map2(.x = benchmark_results, .y = 10^seq(2, 5), .f = ~mutate(tibble(.x), pop_size = .y)) %>%
bind_rows() %>%
mutate(expr = str_remove_all(expr, "\\(.*\\)")) %>%
group_by(expr, pop_size) %>%
mutate(time_seconds = time/10^9) %>%
summarise(fastest_run = min(time_seconds),
average_run = mean(time_seconds),
slowest_run = max(time_seconds))## `summarise()` has grouped output by 'expr'. You can override using the `.groups` argument.benchmark_data %>%
ggplot(aes(y = average_run, x = pop_size)) +
geom_ribbon(aes(ymin = fastest_run, ymax = slowest_run, fill = expr), alpha = .6) +
geom_line(aes(group = expr, col = expr)) +
ylab("Seconds") +
xlab("Rows in the dataset") +
ggtitle("Speed of rowwise operations using different methods") +
theme_blog()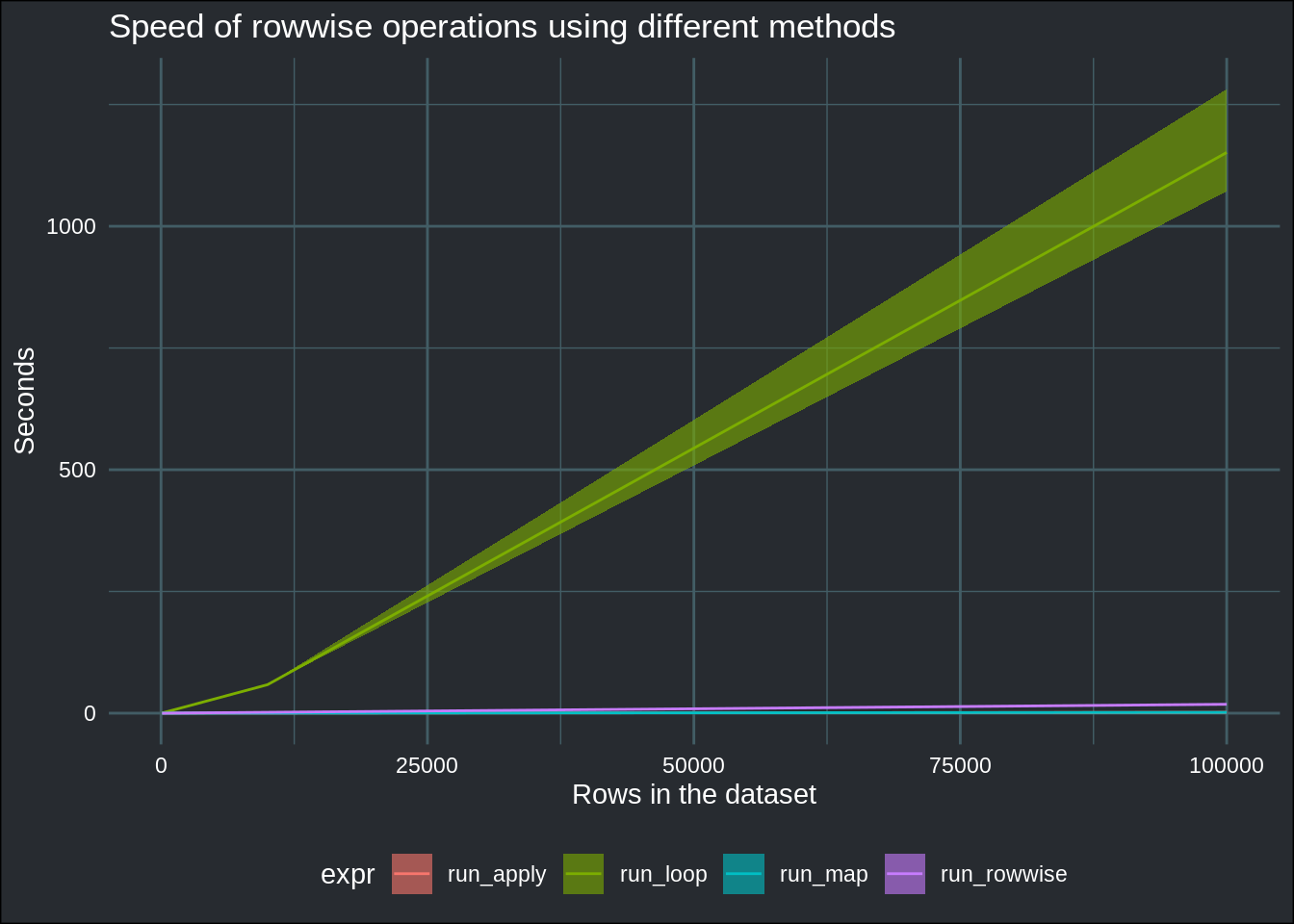
Using a for-loop for row-wise operations is clearly the slowest solution. Let’s take a closer look at the remaining 3 options:
benchmark_data %>%
filter(!grepl("loop", expr)) %>%
ggplot(aes(y = average_run, x = pop_size)) +
geom_ribbon(aes(ymin = fastest_run, ymax = slowest_run, fill = expr), alpha = .6) +
ylab("Seconds") +
xlab("Rows in the dataset") +
ggtitle("Speed of rowwise operations using different methods") +
theme_blog()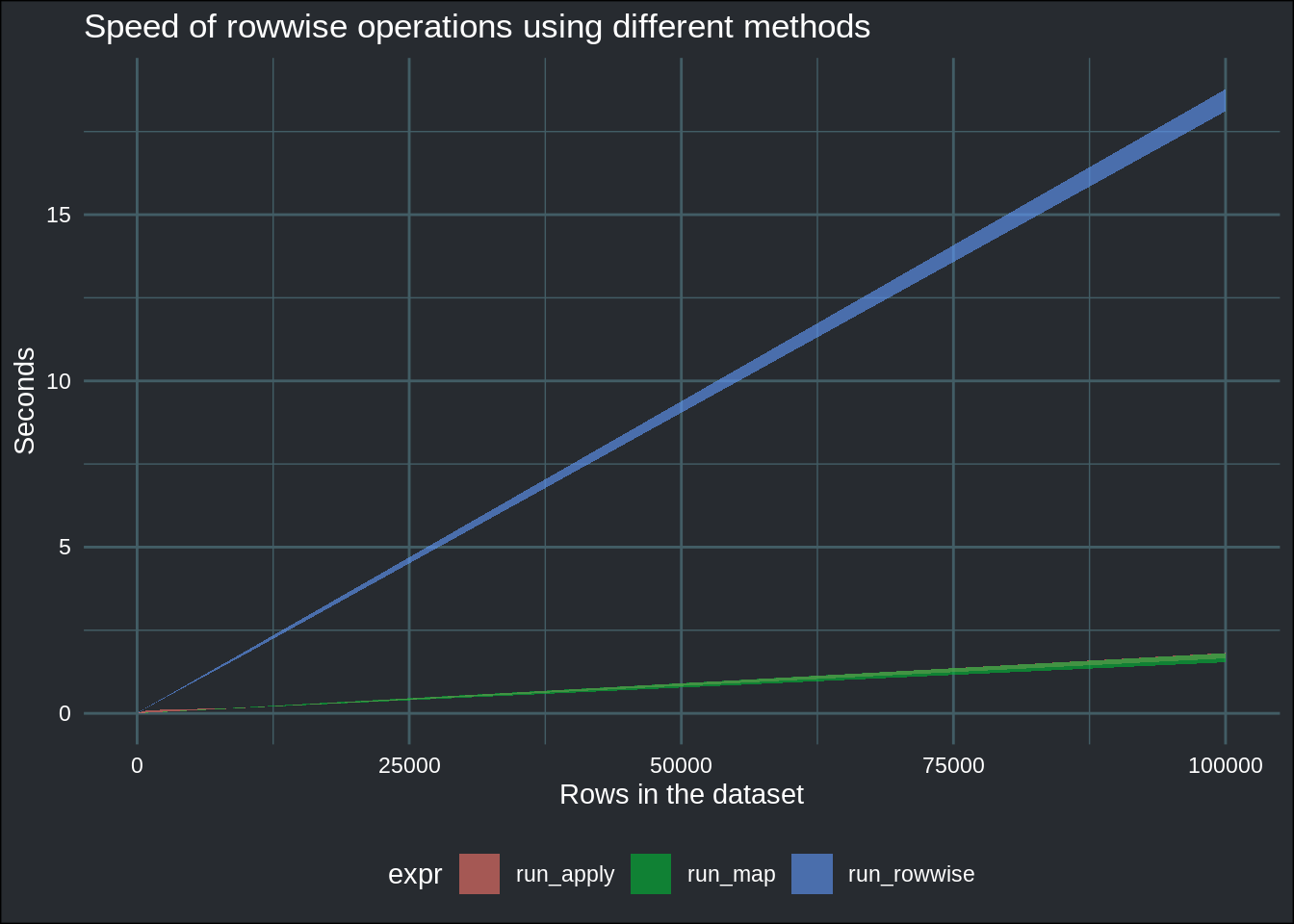
rowwise() loses here, but unless you have to literally run such code hundreds of times, it is still
tolerable. Gives you enough time to browse some memes. But if you have to run such operations
millions of times, you might want to look at either using apply() or the other approach that uses
asplit() and map(). Let’s take a closer look at these two:
benchmark_data %>%
filter(!grepl("loop|rowwise", expr)) %>%
ggplot(aes(y = average_run, x = pop_size)) +
geom_ribbon(aes(ymin = fastest_run, ymax = slowest_run, fill = expr), alpha = .6) +
geom_line(aes(group = expr, col = expr)) +
ylab("Seconds") +
xlab("Rows in the dataset") +
ggtitle("Speed of rowwise operations using different methods") +
theme_blog()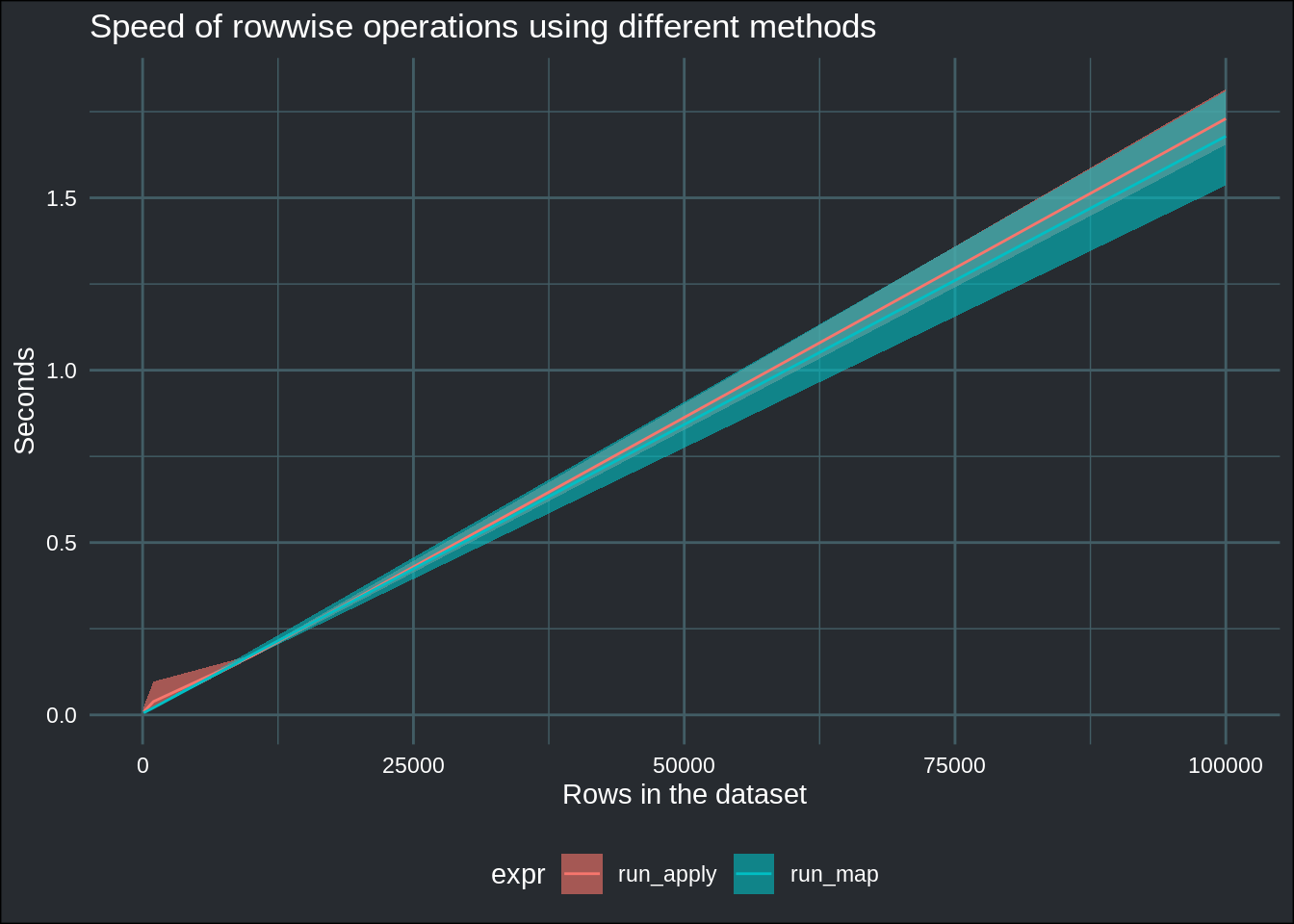
Interestingly, the fastest run using map() was faster than the fastest run using apply(),
but on average, both methods seem to be equivalent. In conclusion, if you need speed and you
need to compute over every column apply() is a clear winner. But if you need row-wise operations,
but only on a subset of columns, rowwise(), even though it is slow, seems to be the only solution.
I wonder if there is a way to use c_across() with the map() approach, and potentially have
the benefits of map() (as fast as apply()) and rowwise() (computing only over certain
columns…). Another subject to explore later.
Part 2 of this blog post is available here
Hope you enjoyed! If you found this blog post useful, you might want to follow me on twitter for blog post updates and buy me an espresso or paypal.me, or buy my ebook on Leanpub. You can also watch my videos on youtube. So much content for you to consoom!