Multiple data imputation and explainability

2019/11/02 R

Introduction

Imputing missing values is quite an important task, but in my experience, very often, it is performed using very simplistic approaches. The basic approach is to impute missing values for numerical features using the average of each feature, or using the mode for categorical features. There are better ways of imputing missing values, for instance by predicting the values using a regression model, or KNN. However, imputing only once is not enough, because each imputed value carries with it a certain level of uncertainty. To account for this, it is better to perform multiple imputation. This means that if you impute your dataset 10 times, you’ll end up with 10 different datasets. Then, you should perform your analysis 10 times, for instance, if training a machine learning model, you should train it on the 10 datasets (and do a train/test split for each, even potentially tune a model for each). Finally, you should pool the results of these 10 analyses.

I have met this approach in the social sciences and statistical literature in general, but very rarely in machine learning. Usually, in the social sciences, explainability is the goal of fitting statistical models to data, and the approach I described above is very well suited for this. Fit 10 (linear) regressions to each imputed dataset, and then pool the estimated coefficients/weights together. Rubin’s rule is used to pool these estimates. You can read more about this rule here. In machine learning, the task is very often prediction; in this case, you should pool the predictions. Computing the average and other statistics of the predictions seem to work just fine in practice.

However, if you are mainly interested in explainability, how should you proceed? I’ve thought a bit about it, and the answer, is “exactly the same way”… I think. What I’m sure about, is you should impute m times, run the analysis m times (which in this case will include getting explanations) and then pool. So the idea is to be able to pool explanations.

Explainability in the “standard” case (no missing values)

To illustrate this idea, I’ll be using the {mice} package for multiple imputation, {h2o} for the machine learning bit and{iml} for explainability. Note that I could have used any other machine learning package instead of {h2o} as {iml} is totally package-agnostic. However, I have been experimenting with {h2o}’s automl implementation lately, so I happened to have code on hand. Let’s start with the “standard” case where the data does not have any missing values.

First let’s load the needed packages and initialize h2o functions with h2o.init():

library(tidyverse)
library(Ecdat)
library(mice)
library(h2o)
library(iml)
h2o.init()

I’ll be using the DoctorContacts data. Here’s a description:

Click to view the description of the data

DoctorContacts              package:Ecdat              R Documentation

Contacts With Medical Doctor

Description:

     a cross-section from 1977-1978

     _number of observations_ : 20186

Usage:

     data(DoctorContacts)
     
Format:

     A time serie containing :

     mdu number of outpatient visits to a medical doctor

     lc log(coinsrate+1) where coinsurance rate is 0 to 100

     idp individual deductible plan ?

     lpi log(annual participation incentive payment) or 0 if no payment

     fmde log(max(medical deductible expenditure)) if IDP=1 and MDE>1
          or 0 otherw

     physlim physical limitation ?

     ndisease number of chronic diseases

     health self-rate health (excellent,good,fair,poor)

     linc log of annual family income (in \$)

     lfam log of family size

     educdec years of schooling of household head

     age exact age

     sex sex (male,female)

     child age less than 18 ?

     black is household head black ?

Source:

     Deb, P.  and P.K.  Trivedi (2002) “The Structure of Demand for
     Medical Care: Latent Class versus Two-Part Models”, _Journal of
     Health Economics_, *21*, 601-625.

References:

     Cameron, A.C.  and P.K.  Trivedi (2005) _Microeconometrics :
     methods and applications_, Cambridge, pp. 553-556 and 565.

The task is to predict "mdu", the number of outpatient visits to an MD. Let’s prepare the data and split it into 3; a training, validation and holdout set.

data("DoctorContacts")

contacts <- as.h2o(DoctorContacts)

splits <- h2o.splitFrame(data=contacts, ratios = c(0.7, 0.2))

original_train <- splits[[1]]

validation <- splits[[2]]

holdout <- splits[[3]]

features_names <- setdiff(colnames(original_train), "mdu")

As you see, the ratios argument c(0.7, 0.2) does not add up to 1. This means that the first of the splits will have 70% of the data, the second split 20% and the final 10% will be the holdout set.

Let’s first go with a poisson regression. To obtain the same results as with R’s built-in glm() function, I use the options below, as per H2o’s glm faq.

If you read Cameron and Trivedi’s Microeconometrics, where this data is presented in the context of count models, you’ll see that they also fit a negative binomial model 2 to this data, as it allows for overdispersion. Here, I’ll stick to a simple poisson regression, simply because the goal of this blog post is not to get the best model; as explained in the beginning, this is an attempt at pooling explanations when doing multiple imputation (and it’s also because GBMs, which I use below, do not handle the negative binomial model).

glm_model <- h2o.glm(y = "mdu", x = features_names,
                     training_frame = original_train,
                     validation_frame = validation,
                     compute_p_values = TRUE,
                     solver = "IRLSM",
                     lambda = 0,
                     remove_collinear_columns = TRUE,
                     score_each_iteration = TRUE,
                     family = "poisson", 
                     link = "log")

Now that I have this simple model, which returns the (almost) same results as R’s glm() function, I can take a look at coefficients and see which are important, because GLMs are easily interpretable:

Click to view h2o.glm()’s output

summary(glm_model)

## Model Details:
## ==============
## 
## H2ORegressionModel: glm
## Model Key:  GLM_model_R_1572735931328_5 
## GLM Model: summary
##    family link regularization number_of_predictors_total
## 1 poisson  log           None                         16
##   number_of_active_predictors number_of_iterations  training_frame
## 1                          16                    5 RTMP_sid_8588_3
## 
## H2ORegressionMetrics: glm
## ** Reported on training data. **
## 
## MSE:  17.6446
## RMSE:  4.200547
## MAE:  2.504063
## RMSLE:  0.8359751
## Mean Residual Deviance :  3.88367
## R^2 :  0.1006768
## Null Deviance :64161.44
## Null D.o.F. :14131
## Residual Deviance :54884.02
## Residual D.o.F. :14115
## AIC :83474.52
## 
## 
## H2ORegressionMetrics: glm
## ** Reported on validation data. **
## 
## MSE:  20.85941
## RMSE:  4.56721
## MAE:  2.574582
## RMSLE:  0.8403465
## Mean Residual Deviance :  4.153042
## R^2 :  0.09933874
## Null Deviance :19667.55
## Null D.o.F. :4078
## Residual Deviance :16940.26
## Residual D.o.F. :4062
## AIC :25273.25
## 
## 
## 
## 
## Scoring History: 
##             timestamp   duration iterations negative_log_likelihood
## 1 2019-11-03 00:33:46  0.000 sec          0             64161.43611
## 2 2019-11-03 00:33:46  0.004 sec          1             56464.99004
## 3 2019-11-03 00:33:46  0.020 sec          2             54935.05581
## 4 2019-11-03 00:33:47  0.032 sec          3             54884.19756
## 5 2019-11-03 00:33:47  0.047 sec          4             54884.02255
## 6 2019-11-03 00:33:47  0.063 sec          5             54884.02255
##   objective
## 1   4.54015
## 2   3.99554
## 3   3.88728
## 4   3.88368
## 5   3.88367
## 6   3.88367
## 
## Variable Importances: (Extract with `h2o.varimp`) 
## =================================================
## 
##        variable relative_importance scaled_importance  percentage
## 1    black.TRUE          0.67756097        1.00000000 0.236627982
## 2   health.poor          0.48287163        0.71266152 0.168635657
## 3  physlim.TRUE          0.33962316        0.50124369 0.118608283
## 4   health.fair          0.25602066        0.37785627 0.089411366
## 5      sex.male          0.19542639        0.28842628 0.068249730
## 6      ndisease          0.16661902        0.24591001 0.058189190
## 7      idp.TRUE          0.15703578        0.23176627 0.054842384
## 8    child.TRUE          0.09988003        0.14741114 0.034881600
## 9          linc          0.09830075        0.14508030 0.034330059
## 10           lc          0.08126160        0.11993253 0.028379394
## 11         lfam          0.07234463        0.10677213 0.025265273
## 12         fmde          0.06622332        0.09773781 0.023127501
## 13      educdec          0.06416087        0.09469387 0.022407220
## 14  health.good          0.05501613        0.08119732 0.019213558
## 15          age          0.03167598        0.04675000 0.011062359
## 16          lpi          0.01938077        0.02860373 0.006768444

As a bonus, let’s see the output of the glm() function:

Click to view glm()’s output

train_tibble <- as_tibble(original_train)

r_glm <- glm(mdu ~ ., data = train_tibble,
            family = poisson(link = "log"))

summary(r_glm)

## 
## Call:
## glm(formula = mdu ~ ., family = poisson(link = "log"), data = train_tibble)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -5.7039  -1.7890  -0.8433   0.4816  18.4703  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  0.0005100  0.0585681   0.009   0.9931    
## lc          -0.0475077  0.0072280  -6.573 4.94e-11 ***
## idpTRUE     -0.1794563  0.0139749 -12.841  < 2e-16 ***
## lpi          0.0129742  0.0022141   5.860 4.63e-09 ***
## fmde        -0.0166968  0.0042265  -3.951 7.80e-05 ***
## physlimTRUE  0.3182780  0.0126868  25.087  < 2e-16 ***
## ndisease     0.0222300  0.0007215  30.811  < 2e-16 ***
## healthfair   0.2434235  0.0192873  12.621  < 2e-16 ***
## healthgood   0.0231824  0.0115398   2.009   0.0445 *  
## healthpoor   0.4608598  0.0329124  14.003  < 2e-16 ***
## linc         0.0826053  0.0062208  13.279  < 2e-16 ***
## lfam        -0.1194981  0.0106904 -11.178  < 2e-16 ***
## educdec      0.0205582  0.0019404  10.595  < 2e-16 ***
## age          0.0041397  0.0005152   8.035 9.39e-16 ***
## sexmale     -0.2096761  0.0104668 -20.032  < 2e-16 ***
## childTRUE    0.1529588  0.0179179   8.537  < 2e-16 ***
## blackTRUE   -0.6231230  0.0176758 -35.253  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 64043  on 14096  degrees of freedom
## Residual deviance: 55529  on 14080  degrees of freedom
## AIC: 84052
## 
## Number of Fisher Scoring iterations: 6

I could also use the excellent {ggeffects} package to see the marginal effects of different variables, for instance "linc":

library(ggeffects)

ggeffect(r_glm, "linc") %>% 
    ggplot(aes(x, predicted)) +
    geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "#0f4150") +
    geom_line(colour = "#82518c") +
    brotools::theme_blog()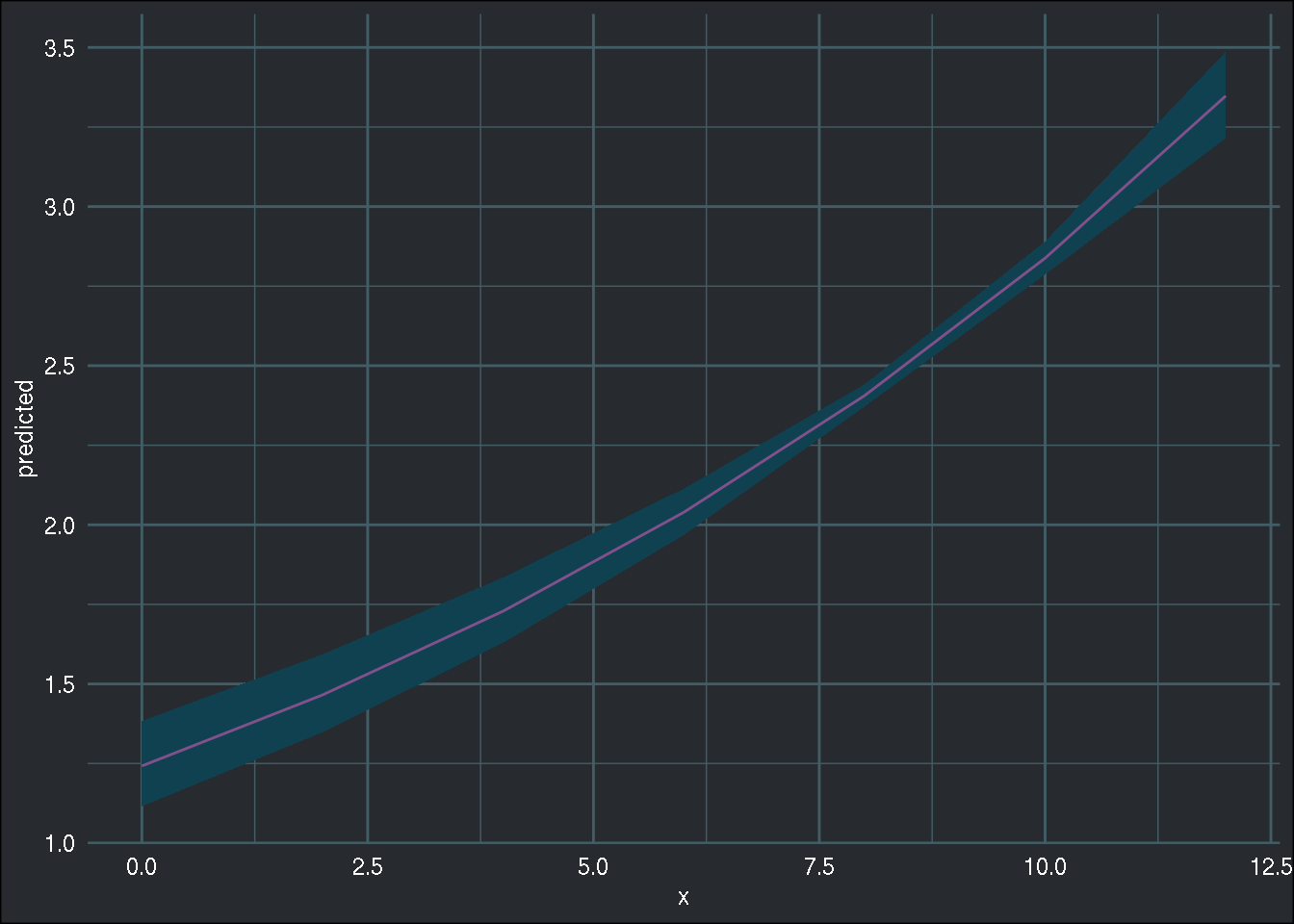

We can see that as “linc” (and other covariates are held constant), the target variable increases.

Let’s also take a look at the marginal effect of a categorical variable, namely "sex":

Click to view another example of marginal effects

library(ggeffects)

ggeffect(r_glm, "sex") %>% 
    ggplot(aes(x, predicted)) +
    geom_point(colour = "#82518c") +
    geom_errorbar(aes(x, ymin = conf.low, ymax = conf.high), colour = "#82518c") +
    brotools::theme_blog()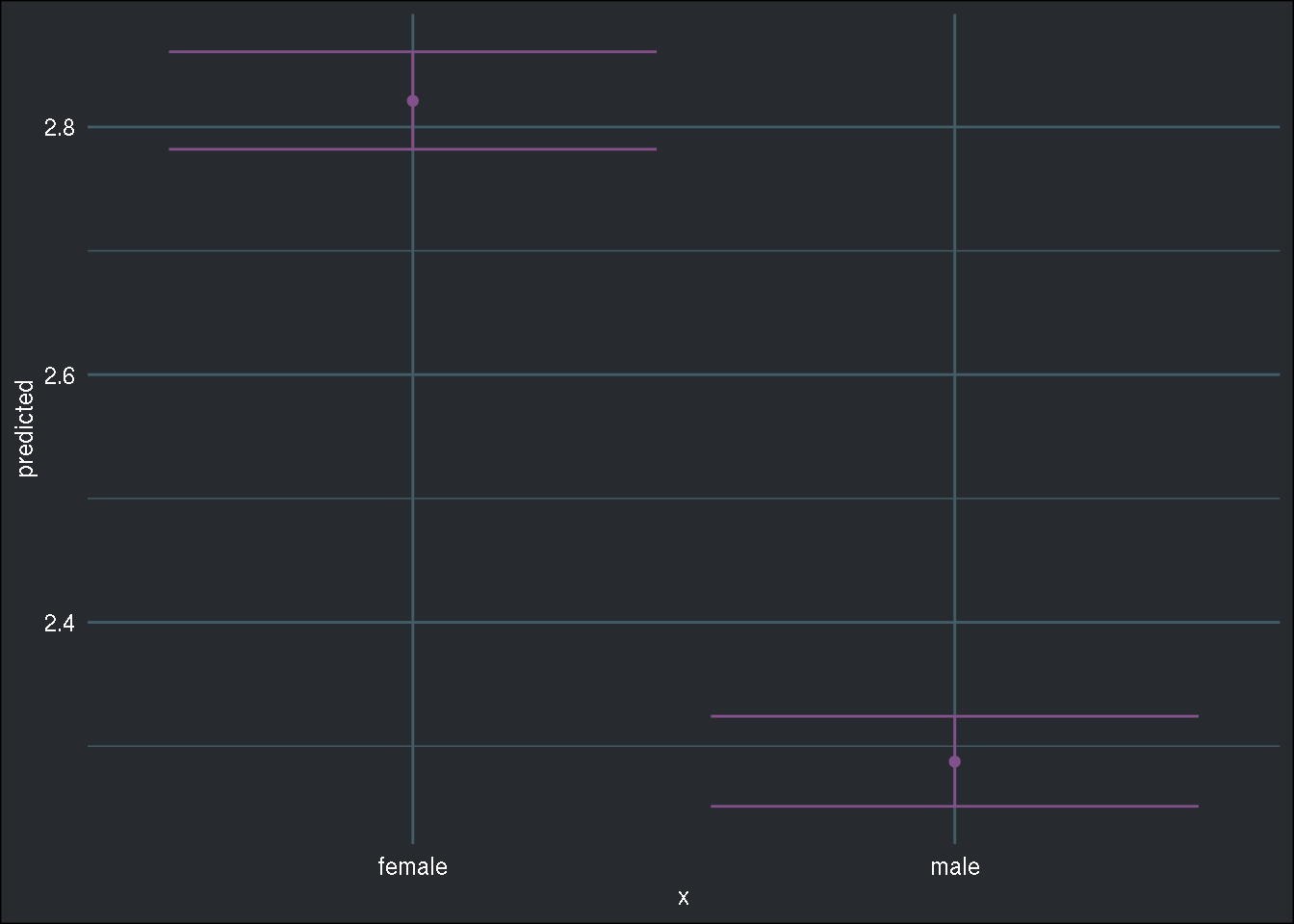

In the case of the "sex" variable, men have significantly less doctor contacts than women.

Now, let’s suppose that I want to train a model with a more complicated name, in order to justify my salary. Suppose I go with one of those nifty black-box models, for instance a GBM, which very likely will perform better than the GLM from before. GBMs are available in {h2o} via the h2o.gbm() function:

gbm_model <- h2o.gbm(y = "mdu", x = features_names,
            training_frame = original_train,
            validation_frame = validation,
            distribution = "poisson",
            score_each_iteration = TRUE,
            ntrees = 110,
            max_depth = 20,
            sample_rate = 0.6,
            col_sample_rate = 0.8,
            col_sample_rate_per_tree = 0.9,
            learn_rate = 0.05)

To find a set of good hyper-parameter values, I actually used h2o.automl() and then used the returned parameter values from the leader model. Maybe I’ll write another blog post about h2o.automl() one day, it’s quite cool. Anyways, now, how do I get me some explainability out of this? The model does perform better than the GLM as indicated by all the different metrics, but now I cannot compute any marginal effects, or anything like that. I do get feature importance by default with:

h2o.varimp(gbm_model)

## Variable Importances: 
##    variable relative_importance scaled_importance percentage
## 1       age       380350.093750          1.000000   0.214908
## 2      linc       282274.343750          0.742143   0.159492
## 3  ndisease       245862.718750          0.646412   0.138919
## 4       lpi       173552.734375          0.456297   0.098062
## 5   educdec       148186.265625          0.389605   0.083729
## 6      lfam       139174.312500          0.365911   0.078637
## 7      fmde        94193.585938          0.247650   0.053222
## 8    health        86160.679688          0.226530   0.048683
## 9       sex        63502.667969          0.166958   0.035881
## 10       lc        50674.968750          0.133232   0.028633
## 11  physlim        45328.382812          0.119175   0.025612
## 12    black        26376.841797          0.069349   0.014904
## 13      idp        24809.185547          0.065227   0.014018
## 14    child         9382.916992          0.024669   0.005302

but that’s it. And had I chosen a different “black-box” model, not based on trees, then I would not even have that. Thankfully, there’s the amazing {iml} package that contains a lot of functions for model-agnostic explanations. If you are not familiar with this package and the methods it implements, I highly encourage you to read the free online ebook written by the packages author, Christoph Molnar (who you can follow on Twitter).

Out of the box, {iml} works with several machine learning frameworks, such as {caret} or {mlr} but not with {h2o}. However, this is not an issue; you only need to create a predict function which returns a data frame (h2o.predict() used for prediction with h2o models returns an h2o frame). I have found this interesting blog post from business-science.io which explains how to do this. I highly recommend you read this blog post, as it goes much deeper into the capabilities of {iml}.

So let’s write a predict function that {iml} can use:

#source: https://www.business-science.io/business/2018/08/13/iml-model-interpretability.html
predict_for_iml <- function(model, newdata){
  as_tibble(h2o.predict(model, as.h2o(newdata)))
}

And let’s now create a Predictor object. These objects are used by {iml} to create explanations:

just_features <- as_tibble(holdout[, 2:15])
actual_target <- as_tibble(holdout[, 1])

predictor_original <- Predictor$new(
  model = gbm_model, 
  data = just_features, 
  y = actual_target, 
  predict.fun = predict_for_iml
  )

predictor_original can now be used to compute all kinds of explanations. I won’t go into much detail here, as this blog post is already quite long (and I haven’t even reached what I actually want to write about yet) and you can read more on the before-mentioned blog post or directly from Christoph Molnar’s ebook linked above.

First, let’s compute a partial dependence plot, which shows the marginal effect of a variable on the outcome. This is to compare it to the one from the GLM model:

feature_effect_original <- FeatureEffect$new(predictor_original, "linc", method = "pdp")

plot(feature_effect_original) +
    brotools::theme_blog()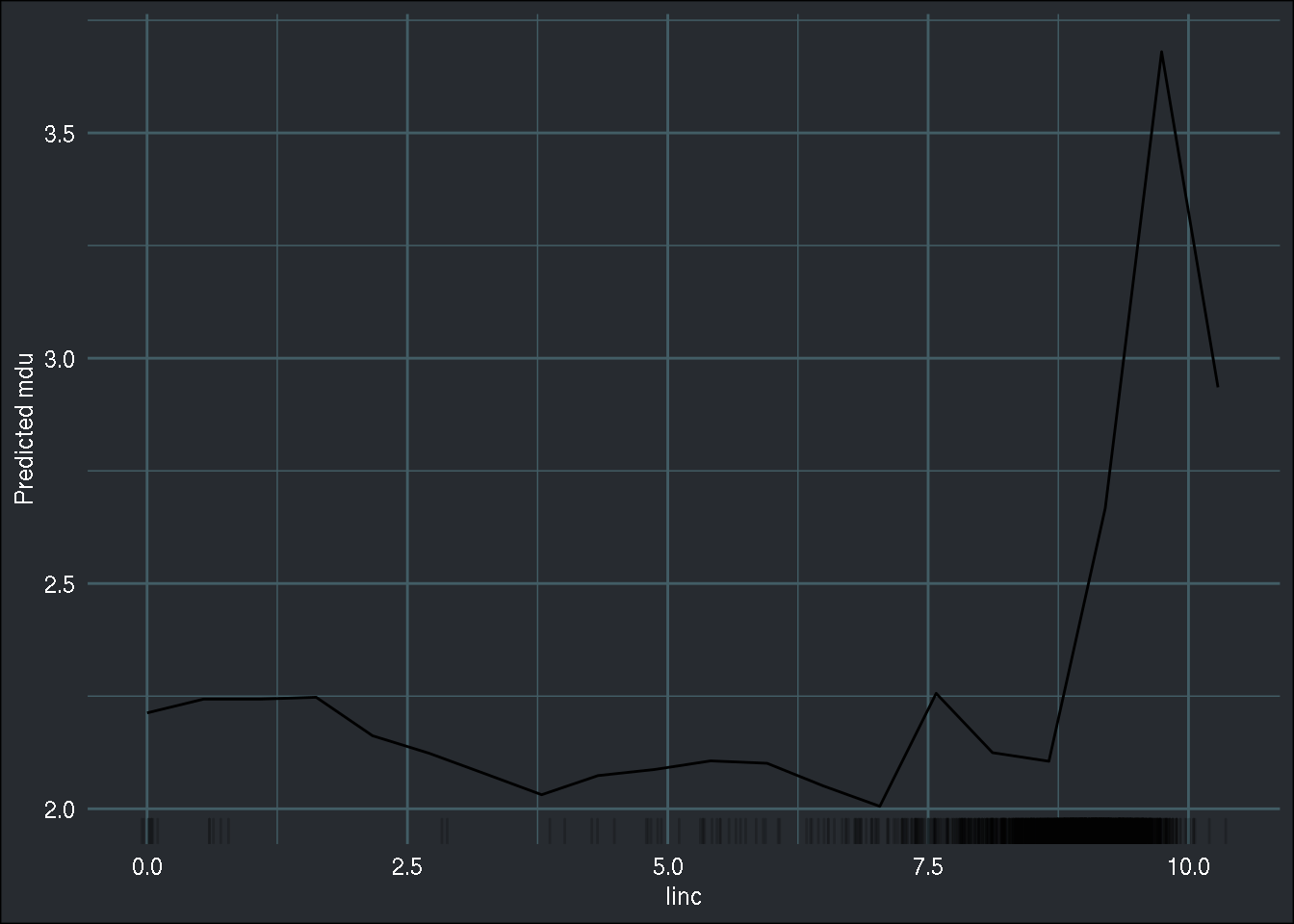

feature_effect_original <- FeatureEffect$new(predictor_original, "linc", method = "pdp")

plot(feature_effect_original) +
    brotools::theme_blog()

Quite similar to the marginal effects from the GLM! Let’s now compute model-agnostic feature importances:

feature_importance_original <- FeatureImp$new(predictor_original, loss = "mse")

plot(feature_importance_original)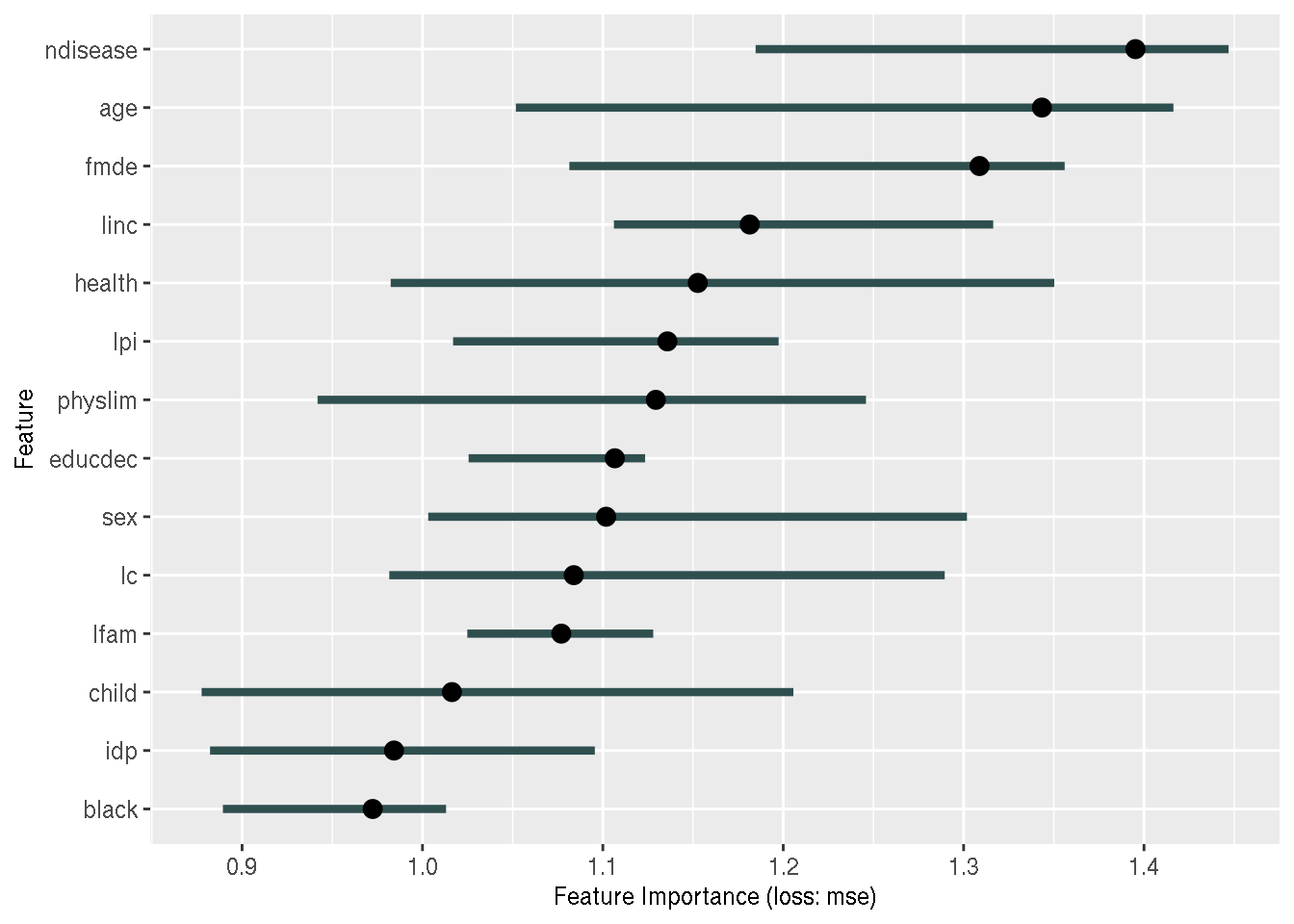

And finally, the interaction effect of the sex variable interacted with all the others:

interaction_sex_original <- Interaction$new(predictor_original, feature = "sex")

plot(interaction_sex_original)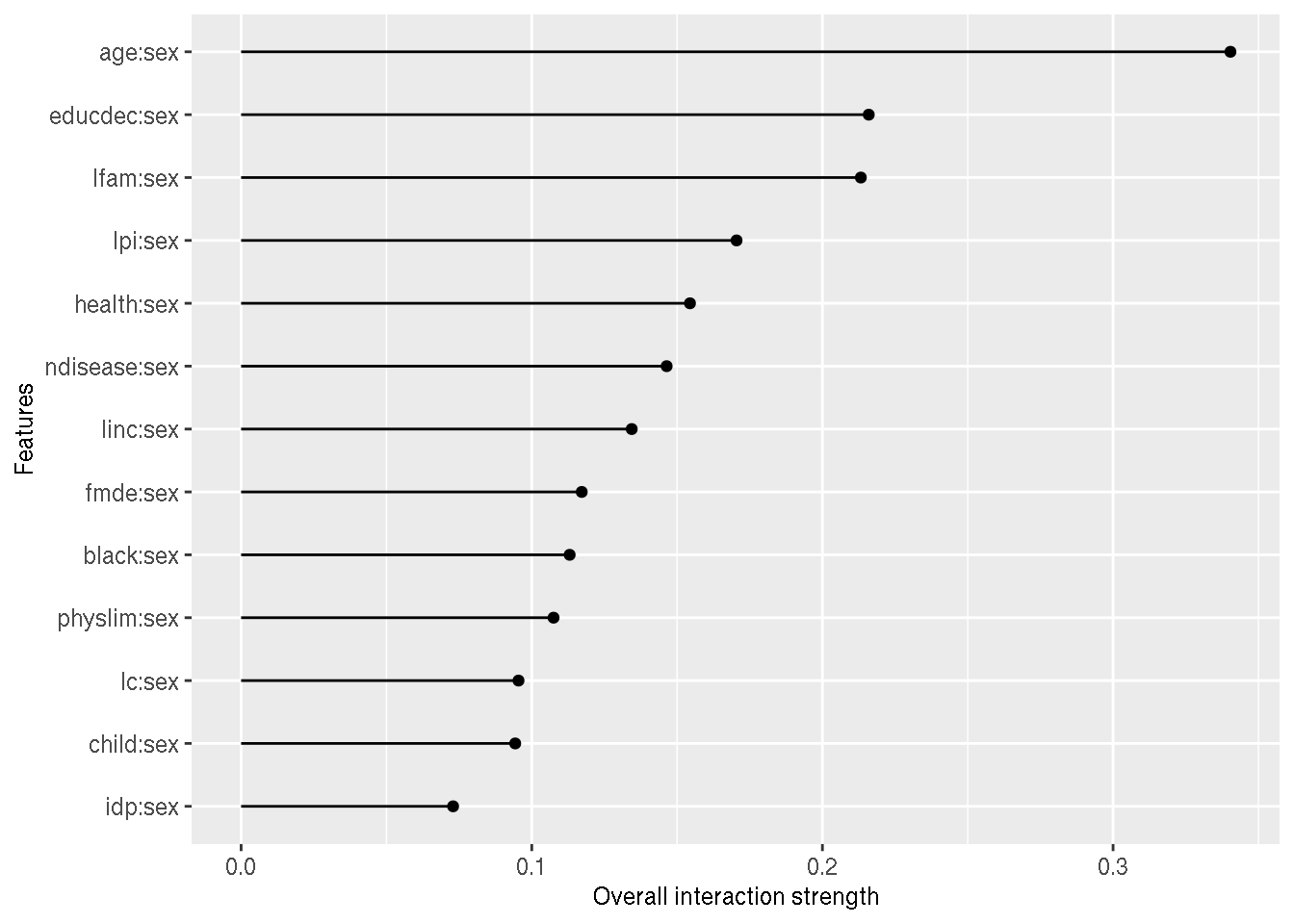

Ok so let’s assume that I’m happy with these explanations, and do need or want to go further. This would be the end of it in an ideal world, but this is not an ideal world unfortunately, but it’s the best we’ve got. In the real world, it often happens that data comes with missing values.

Missing data and explainability

As explained in the beginning, I’ve been wondering how to deal with missing values when the goal of the analysis is explainability. How can the explanations be pooled? Let’s start with creating a data set with missing values, then perform multiple imputation, then perform the analysis.

First, let me create a patterns matrix, that I will pass to the ampute() function from the {mice} package. This function creates a dataset with missing values, and by using its patterns argument, I can decide which columns should have missing values:

patterns <- -1*(diag(1, nrow = 15, ncol = 15) - 1)

patterns[ ,c(seq(1, 6), c(9, 13))] <- 0

amputed_train <- ampute(as_tibble(original_train), prop = 0.1, patterns = patterns, mech = "MNAR")

## Warning: Data is made numeric because the calculation of weights requires
## numeric data

Let’s take a look at the missingness pattern:

naniar::vis_miss(amputed_train$amp) + 
    brotools::theme_blog() + 
      theme(axis.text.x=element_text(angle=90, hjust=1))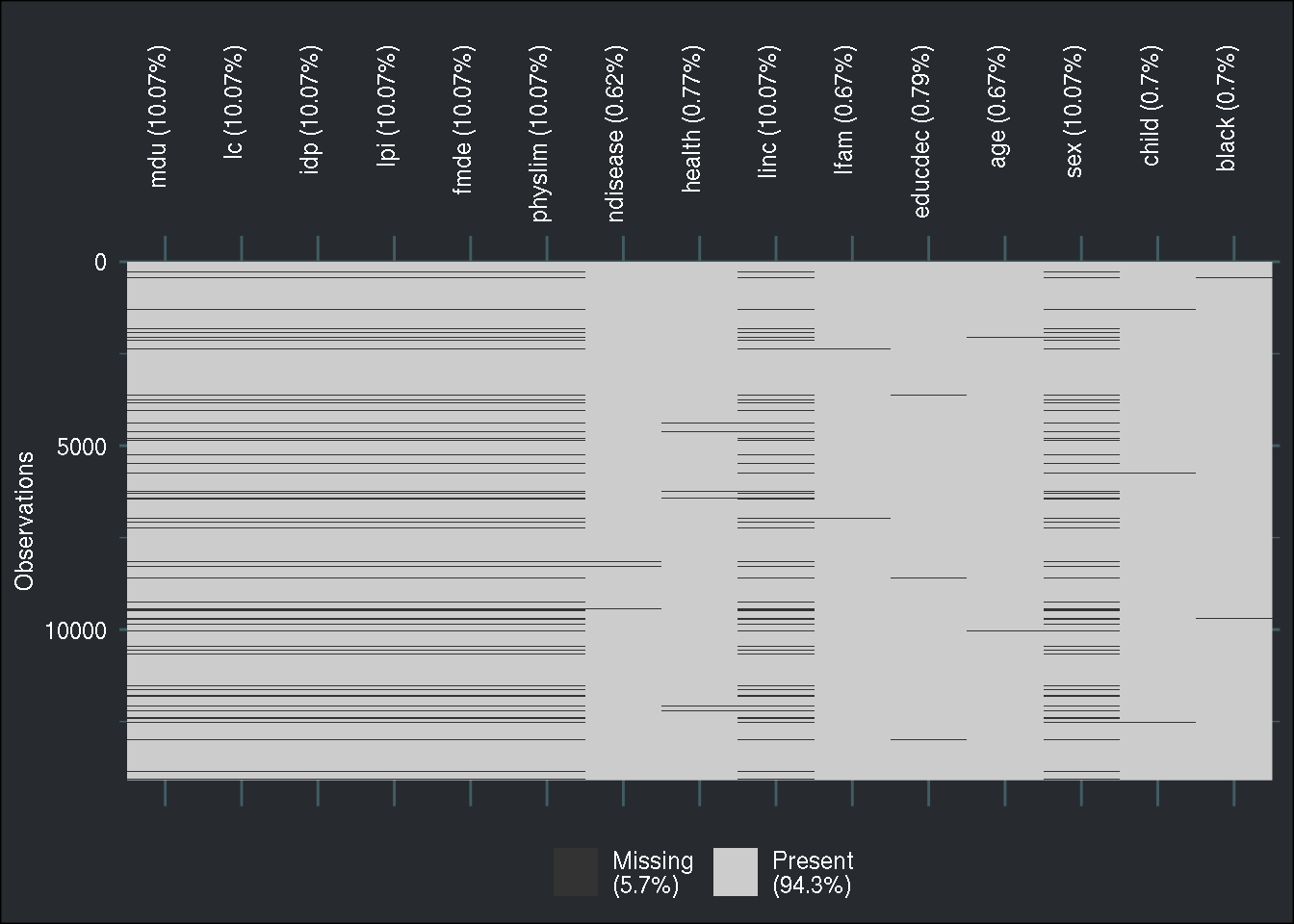

Ok, so now let’s suppose that this was the dataset I was given. As a serious data scientist, I decide to perform multiple imputation first:

imputed_train_data <- mice(data = amputed_train$amp, m = 10)

long_train_data <- complete(imputed_train_data, "long")

So because I performed multiple imputation 10 times, I now have 10 different datasets. I should now perform my analysis on these 10 datasets, which means I should run my GBM on each of them, and then get out the explanations for each of them. So let’s do just that. But first, let’s change the columns back to how they were; to perform amputation, the factor columns were converted to numbers:

long_train_data <- long_train_data %>% 
    mutate(idp = ifelse(idp == 1, FALSE, TRUE),
           physlim = ifelse(physlim == 1, FALSE, TRUE),
           health = as.factor(case_when(health == 1 ~ "excellent",
                              health == 2 ~ "fair",
                              health == 3 ~ "good", 
                              health == 4 ~  "poor")),
           sex = as.factor(ifelse(sex == 1, "female", "male")),
           child = ifelse(child == 1, FALSE, TRUE),
           black = ifelse(black == 1, FALSE, TRUE))

Ok, so now we’re ready to go. I will use the h2o.gbm() function on each imputed data set. For this, I’ll use the group_by()-nest() trick which consists in grouping the dataset by the .imp column, then nesting it, then mapping the h2o.gbm() function to each imputed dataset. If you are not familiar with this, you can read this other blog post, which explains the approach. I define a custom function, train_on_imputed_data() to run h2o.gbm() on each imputed data set:

train_on_imputed_data <- function(long_data){
    long_data %>% 
        group_by(.imp) %>% 
        nest() %>% 
        mutate(model = map(data, ~h2o.gbm(y = "mdu", x = features_names,
            training_frame = as.h2o(.),
            validation_frame = validation,
            distribution = "poisson",
            score_each_iteration = TRUE,
            ntrees = 110,
            max_depth = 20,
            sample_rate = 0.6,
            col_sample_rate = 0.8,
            col_sample_rate_per_tree = 0.9,
            learn_rate = 0.05)))
}

Now the training takes place:

imp_trained <- train_on_imputed_data(long_train_data)

Let’s take a look at imp_trained:

imp_trained

## # A tibble: 10 x 3
## # Groups:   .imp [10]
##     .imp            data model     
##    <int> <list<df[,16]>> <list>    
##  1     1   [14,042 × 16] <H2ORgrsM>
##  2     2   [14,042 × 16] <H2ORgrsM>
##  3     3   [14,042 × 16] <H2ORgrsM>
##  4     4   [14,042 × 16] <H2ORgrsM>
##  5     5   [14,042 × 16] <H2ORgrsM>
##  6     6   [14,042 × 16] <H2ORgrsM>
##  7     7   [14,042 × 16] <H2ORgrsM>
##  8     8   [14,042 × 16] <H2ORgrsM>
##  9     9   [14,042 × 16] <H2ORgrsM>
## 10    10   [14,042 × 16] <H2ORgrsM>

We see that the column model contains one model for each imputed dataset. Now comes the part I wanted to write about (finally): getting explanations out of this. Getting the explanations from each model is not the hard part, that’s easily done using some {tidyverse} magic (if you’re following along, run this bit of code below, and go make dinner, have dinner, and wash the dishes, because it takes time to run):

make_predictors <- function(model){
    Predictor$new(
        model = model, 
        data = just_features, 
        y = actual_target, 
        predict.fun = predict_for_iml
        )
}

make_effect <- function(predictor_object, feature = "linc", method = "pdp"){
    FeatureEffect$new(predictor_object, feature, method)
}

make_feat_imp <- function(predictor_object, loss = "mse"){
    FeatureImp$new(predictor_object, loss)
}

make_interactions <- function(predictor_object, feature = "sex"){
    Interaction$new(predictor_object, feature = feature)
}

imp_trained <- imp_trained %>%
    mutate(predictors = map(model, make_predictors)) %>% 
    mutate(effect_linc = map(predictors, make_effect)) %>% 
    mutate(feat_imp = map(predictors, make_feat_imp)) %>% 
    mutate(interactions_sex = map(predictors, make_interactions))

Ok so now that I’ve got these explanations, I am done with my analysis. This is the time to pool the results together. Remember, in the case of regression models as used in the social sciences, this means averaging the estimated model parameters and using Rubin’s rule to compute their standard errors. But in this case, this is not so obvious. Should the explanations be averaged? Should I instead analyse them one by one, and see if they differ? My gut feeling is that they shouldn’t differ much, but who knows? Perhaps the answer is doing a bit of both. I have checked online for a paper that would shed some light into this, but have not found any. So let’s take a closer look to the explanations. Let’s look at feature importance:

Click to view the 10 feature importances

imp_trained %>% 
    pull(feat_imp)

## [[1]]
## Interpretation method:  FeatureImp 
## error function: mse
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##    feature importance.05 importance importance.95 permutation.error
## 1 ndisease     1.0421605   1.362672      1.467244          22.03037
## 2     fmde     0.8611917   1.142809      1.258692          18.47583
## 3      lpi     0.8706659   1.103367      1.196081          17.83817
## 4   health     0.8941010   1.098014      1.480508          17.75164
## 5       lc     0.8745229   1.024288      1.296668          16.55970
## 6    black     0.7537278   1.006294      1.095054          16.26879
## 
## [[2]]
## Interpretation method:  FeatureImp 
## error function: mse
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##    feature importance.05 importance importance.95 permutation.error
## 1      age      0.984304   1.365702      1.473146          22.52529
## 2     linc      1.102023   1.179169      1.457907          19.44869
## 3 ndisease      1.075821   1.173938      1.642938          19.36241
## 4     fmde      1.059303   1.150112      1.281291          18.96944
## 5       lc      0.837573   1.132719      1.200556          18.68257
## 6  physlim      0.763757   1.117635      1.644434          18.43379
## 
## [[3]]
## Interpretation method:  FeatureImp 
## error function: mse
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##    feature importance.05 importance importance.95 permutation.error
## 1      age     0.8641304   1.334382      1.821797          21.62554
## 2    black     1.0553001   1.301338      1.429119          21.09001
## 3     fmde     0.8965085   1.208761      1.360217          19.58967
## 4 ndisease     1.0577766   1.203418      1.651611          19.50309
## 5     linc     0.9299725   1.114041      1.298379          18.05460
## 6      sex     0.9854144   1.091391      1.361406          17.68754
## 
## [[4]]
## Interpretation method:  FeatureImp 
## error function: mse
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##   feature importance.05 importance importance.95 permutation.error
## 1 educdec     0.9469049   1.263961      1.358115          20.52909
## 2     age     1.0980269   1.197441      1.763202          19.44868
## 3  health     0.8539843   1.133338      1.343389          18.40753
## 4    linc     0.7608811   1.123423      1.328756          18.24649
## 5     lpi     0.8203850   1.103394      1.251688          17.92118
## 6   black     0.9476909   1.089861      1.328960          17.70139
## 
## [[5]]
## Interpretation method:  FeatureImp 
## error function: mse
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##   feature importance.05 importance importance.95 permutation.error
## 1     lpi     0.9897789   1.336405      1.601778          22.03791
## 2 educdec     0.8701162   1.236741      1.424602          20.39440
## 3     age     0.8537786   1.181242      1.261411          19.47920
## 4    lfam     1.0185313   1.133158      1.400151          18.68627
## 5     idp     0.9502284   1.069772      1.203147          17.64101
## 6    linc     0.8600586   1.042453      1.395231          17.19052
## 
## [[6]]
## Interpretation method:  FeatureImp 
## error function: mse
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##   feature importance.05 importance importance.95 permutation.error
## 1      lc     0.7707383   1.208190      1.379422          19.65436
## 2     sex     0.9309901   1.202629      1.479511          19.56391
## 3    linc     1.0549563   1.138404      1.624217          18.51912
## 4     lpi     0.9360817   1.135198      1.302084          18.46696
## 5 physlim     0.7357272   1.132525      1.312584          18.42349
## 6   child     1.0199964   1.109120      1.316306          18.04274
## 
## [[7]]
## Interpretation method:  FeatureImp 
## error function: mse
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##    feature importance.05 importance importance.95 permutation.error
## 1     linc     0.9403425   1.262994      1.511122          20.65942
## 2       lc     1.0481333   1.233136      1.602796          20.17103
## 3 ndisease     1.1612194   1.212454      1.320208          19.83272
## 4  educdec     0.7924637   1.197343      1.388218          19.58554
## 5     lfam     0.8423790   1.178545      1.349884          19.27805
## 6      age     0.9125829   1.168297      1.409525          19.11043
## 
## [[8]]
## Interpretation method:  FeatureImp 
## error function: mse
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##    feature importance.05 importance importance.95 permutation.error
## 1      age     1.1281736   1.261273      1.609524          20.55410
## 2   health     0.9134557   1.240597      1.432366          20.21716
## 3     lfam     0.7469043   1.182294      1.345910          19.26704
## 4      lpi     0.8088552   1.160863      1.491139          18.91779
## 5 ndisease     1.0756671   1.104357      1.517278          17.99695
## 6     fmde     0.6929092   1.093465      1.333544          17.81946
## 
## [[9]]
## Interpretation method:  FeatureImp 
## error function: mse
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##    feature importance.05 importance importance.95 permutation.error
## 1  educdec     1.0188109   1.287697      1.381982          20.92713
## 2      lpi     0.9853336   1.213095      1.479002          19.71473
## 3     linc     0.8354715   1.195344      1.254350          19.42625
## 4      age     0.9980451   1.179371      1.383545          19.16666
## 5 ndisease     1.0492685   1.176804      1.397398          19.12495
## 6     lfam     1.0814043   1.166626      1.264592          18.95953
## 
## [[10]]
## Interpretation method:  FeatureImp 
## error function: mse
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##    feature importance.05 importance importance.95 permutation.error
## 1      age     0.9538824   1.211869      1.621151          19.53671
## 2      sex     0.9148921   1.211253      1.298311          19.52678
## 3     lfam     0.8227355   1.093094      1.393815          17.62192
## 4 ndisease     0.8282127   1.090779      1.205994          17.58459
## 5       lc     0.7004401   1.060870      1.541697          17.10244
## 6   health     0.8137149   1.058324      1.183639          17.06138

As you can see, the feature importances are quite different from each other, but I don’t think this comes from the imputations, but rather from the fact that feature importance depends on shuffling the feature, which adds randomness to the measurement (source: https://christophm.github.io/interpretable-ml-book/feature-importance.html#disadvantages-9). To mitigate this, Christoph Molnar suggests repeating the the permutation and averaging the importance measures; I think that this would be my approach for pooling as well.

Let’s now take a look at interactions:

Click to view the 10 interactions

imp_trained %>% 
    pull(interactions_sex)

## [[1]]
## Interpretation method:  Interaction 
## 
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##       .feature .interaction
## 1       lc:sex   0.07635197
## 2      idp:sex   0.08172754
## 3      lpi:sex   0.10704357
## 4     fmde:sex   0.11267146
## 5  physlim:sex   0.04099073
## 6 ndisease:sex   0.16314524
## 
## [[2]]
## Interpretation method:  Interaction 
## 
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##       .feature .interaction
## 1       lc:sex   0.10349820
## 2      idp:sex   0.07432519
## 3      lpi:sex   0.11651413
## 4     fmde:sex   0.18123926
## 5  physlim:sex   0.12952808
## 6 ndisease:sex   0.14528876
## 
## [[3]]
## Interpretation method:  Interaction 
## 
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##       .feature .interaction
## 1       lc:sex   0.05919320
## 2      idp:sex   0.05586197
## 3      lpi:sex   0.24253335
## 4     fmde:sex   0.05240474
## 5  physlim:sex   0.06404969
## 6 ndisease:sex   0.14508072
## 
## [[4]]
## Interpretation method:  Interaction 
## 
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##       .feature .interaction
## 1       lc:sex   0.02775529
## 2      idp:sex   0.02050390
## 3      lpi:sex   0.11781130
## 4     fmde:sex   0.11084240
## 5  physlim:sex   0.17932694
## 6 ndisease:sex   0.07181589
## 
## [[5]]
## Interpretation method:  Interaction 
## 
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##       .feature .interaction
## 1       lc:sex   0.12873151
## 2      idp:sex   0.03681428
## 3      lpi:sex   0.15879389
## 4     fmde:sex   0.16952900
## 5  physlim:sex   0.07031520
## 6 ndisease:sex   0.10567463
## 
## [[6]]
## Interpretation method:  Interaction 
## 
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##       .feature .interaction
## 1       lc:sex   0.15320481
## 2      idp:sex   0.08645037
## 3      lpi:sex   0.16674641
## 4     fmde:sex   0.14671054
## 5  physlim:sex   0.09236257
## 6 ndisease:sex   0.14605618
## 
## [[7]]
## Interpretation method:  Interaction 
## 
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##       .feature .interaction
## 1       lc:sex   0.04072960
## 2      idp:sex   0.05641868
## 3      lpi:sex   0.19491959
## 4     fmde:sex   0.07119644
## 5  physlim:sex   0.05777469
## 6 ndisease:sex   0.16555363
## 
## [[8]]
## Interpretation method:  Interaction 
## 
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##       .feature .interaction
## 1       lc:sex   0.04979709
## 2      idp:sex   0.06036898
## 3      lpi:sex   0.14009307
## 4     fmde:sex   0.10927688
## 5  physlim:sex   0.08761533
## 6 ndisease:sex   0.20544585
## 
## [[9]]
## Interpretation method:  Interaction 
## 
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##       .feature .interaction
## 1       lc:sex   0.08572075
## 2      idp:sex   0.12254979
## 3      lpi:sex   0.17532347
## 4     fmde:sex   0.12557420
## 5  physlim:sex   0.05084209
## 6 ndisease:sex   0.13977328
## 
## [[10]]
## Interpretation method:  Interaction 
## 
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##       .feature .interaction
## 1       lc:sex   0.08636490
## 2      idp:sex   0.04807331
## 3      lpi:sex   0.17922280
## 4     fmde:sex   0.05728403
## 5  physlim:sex   0.09392774
## 6 ndisease:sex   0.13408956

It would seem that interactions are a bit more stable. Let’s average the values; for this I need to access the results element of the interactions object and the result out:

interactions_sex_result <- imp_trained %>% 
    mutate(interactions_results = map(interactions_sex, function(x)(x$results))) %>% 
    pull()

interactions_sex_result is a list of dataframes, which means I can bind the rows together and compute whatever I need:

interactions_sex_result %>% 
    bind_rows() %>% 
    group_by(.feature) %>% 
    summarise_at(.vars = vars(.interaction), 
                 .funs = funs(mean, sd, low_ci = quantile(., 0.05), high_ci = quantile(., 0.95)))

## # A tibble: 13 x 5
##    .feature       mean     sd low_ci high_ci
##    <chr>         <dbl>  <dbl>  <dbl>   <dbl>
##  1 age:sex      0.294  0.0668 0.181    0.369
##  2 black:sex    0.117  0.0286 0.0763   0.148
##  3 child:sex    0.0817 0.0308 0.0408   0.125
##  4 educdec:sex  0.148  0.0411 0.104    0.220
##  5 fmde:sex     0.114  0.0443 0.0546   0.176
##  6 health:sex   0.130  0.0190 0.104    0.151
##  7 idp:sex      0.0643 0.0286 0.0278   0.106
##  8 lc:sex       0.0811 0.0394 0.0336   0.142
##  9 lfam:sex     0.149  0.0278 0.125    0.198
## 10 linc:sex     0.142  0.0277 0.104    0.179
## 11 lpi:sex      0.160  0.0416 0.111    0.221
## 12 ndisease:sex 0.142  0.0356 0.0871   0.187
## 13 physlim:sex  0.0867 0.0415 0.0454   0.157

That seems pretty good. Now, what about the partial dependence? Let’s take a closer look:

Click to view the 10 pdps

imp_trained %>% 
    pull(effect_linc)

## [[1]]
## Interpretation method:  FeatureEffect 
## features: linc[numerical]
## grid size: 20
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##        linc   .y.hat .type
## 1 0.0000000 1.652445   pdp
## 2 0.5312226 1.687522   pdp
## 3 1.0624453 1.687522   pdp
## 4 1.5936679 1.687522   pdp
## 5 2.1248905 1.685088   pdp
## 6 2.6561132 1.694112   pdp
## 
## [[2]]
## Interpretation method:  FeatureEffect 
## features: linc[numerical]
## grid size: 20
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##        linc   .y.hat .type
## 1 0.0000000 1.813449   pdp
## 2 0.5312226 1.816195   pdp
## 3 1.0624453 1.816195   pdp
## 4 1.5936679 1.816195   pdp
## 5 2.1248905 1.804457   pdp
## 6 2.6561132 1.797238   pdp
## 
## [[3]]
## Interpretation method:  FeatureEffect 
## features: linc[numerical]
## grid size: 20
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##        linc   .y.hat .type
## 1 0.0000000 1.906515   pdp
## 2 0.5312226 2.039318   pdp
## 3 1.0624453 2.039318   pdp
## 4 1.5936679 2.039318   pdp
## 5 2.1248905 2.002970   pdp
## 6 2.6561132 2.000922   pdp
## 
## [[4]]
## Interpretation method:  FeatureEffect 
## features: linc[numerical]
## grid size: 20
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##        linc   .y.hat .type
## 1 0.0000000 1.799552   pdp
## 2 0.5312226 2.012634   pdp
## 3 1.0624453 2.012634   pdp
## 4 1.5936679 2.012634   pdp
## 5 2.1248905 1.982425   pdp
## 6 2.6561132 1.966392   pdp
## 
## [[5]]
## Interpretation method:  FeatureEffect 
## features: linc[numerical]
## grid size: 20
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##        linc   .y.hat .type
## 1 0.0000000 1.929158   pdp
## 2 0.5312226 1.905171   pdp
## 3 1.0624453 1.905171   pdp
## 4 1.5936679 1.905171   pdp
## 5 2.1248905 1.879721   pdp
## 6 2.6561132 1.869113   pdp
## 
## [[6]]
## Interpretation method:  FeatureEffect 
## features: linc[numerical]
## grid size: 20
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##        linc   .y.hat .type
## 1 0.0000000 2.147697   pdp
## 2 0.5312226 2.162393   pdp
## 3 1.0624453 2.162393   pdp
## 4 1.5936679 2.162393   pdp
## 5 2.1248905 2.119923   pdp
## 6 2.6561132 2.115131   pdp
## 
## [[7]]
## Interpretation method:  FeatureEffect 
## features: linc[numerical]
## grid size: 20
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##        linc   .y.hat .type
## 1 0.0000000 1.776742   pdp
## 2 0.5312226 1.957938   pdp
## 3 1.0624453 1.957938   pdp
## 4 1.5936679 1.957938   pdp
## 5 2.1248905 1.933847   pdp
## 6 2.6561132 1.885287   pdp
## 
## [[8]]
## Interpretation method:  FeatureEffect 
## features: linc[numerical]
## grid size: 20
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##        linc   .y.hat .type
## 1 0.0000000 2.020647   pdp
## 2 0.5312226 2.017981   pdp
## 3 1.0624453 2.017981   pdp
## 4 1.5936679 2.017981   pdp
## 5 2.1248905 1.981122   pdp
## 6 2.6561132 2.017604   pdp
## 
## [[9]]
## Interpretation method:  FeatureEffect 
## features: linc[numerical]
## grid size: 20
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##        linc   .y.hat .type
## 1 0.0000000 1.811189   pdp
## 2 0.5312226 2.003053   pdp
## 3 1.0624453 2.003053   pdp
## 4 1.5936679 2.003053   pdp
## 5 2.1248905 1.938150   pdp
## 6 2.6561132 1.918518   pdp
## 
## [[10]]
## Interpretation method:  FeatureEffect 
## features: linc[numerical]
## grid size: 20
## 
## Analysed predictor: 
## Prediction task: unknown 
## 
## 
## Analysed data:
## Sampling from data.frame with 2013 rows and 14 columns.
## 
## Head of results:
##        linc   .y.hat .type
## 1 0.0000000 1.780325   pdp
## 2 0.5312226 1.850203   pdp
## 3 1.0624453 1.850203   pdp
## 4 1.5936679 1.850203   pdp
## 5 2.1248905 1.880805   pdp
## 6 2.6561132 1.881305   pdp

As you can see, the values are quite similar. I think that in the case of plots, the best way to visualize the impact of the imputation is to simply plot all the lines in a single plot:

effect_linc_results <- imp_trained %>% 
    mutate(effect_linc_results = map(effect_linc, function(x)(x$results))) %>% 
    select(.imp, effect_linc_results) %>% 
    unnest(effect_linc_results)

effect_linc_results %>% 
    bind_rows() %>% 
    ggplot() + 
    geom_line(aes(y = .y.hat, x = linc, group = .imp), colour = "#82518c") + 
    brotools::theme_blog()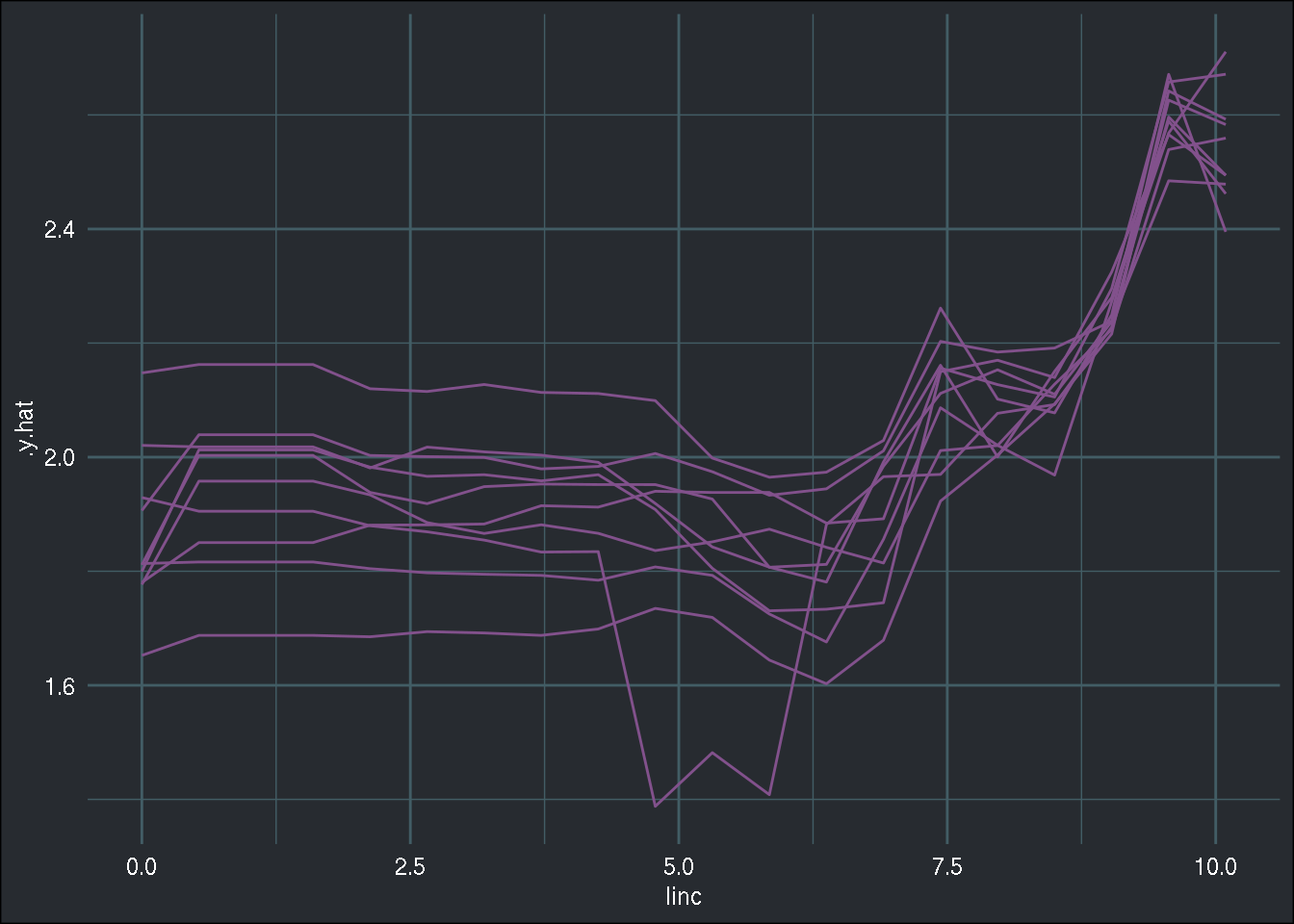

Overall, the partial dependence plot seems to behave in a very similar way across the different imputed datasets!

To conclude, I think that the approach I suggest here is nothing revolutionary; it is consistent with the way one should conduct an analysis with multiple imputed datasets. However, the pooling step is non-trivial and there is no magic recipe; it really depends on the goal of the analysis and what you want or need to show.

Hope you enjoyed! If you found this blog post useful, you might want to follow me on twitter for blog post updates and buy me an espresso or paypal.me, or buy my ebook on Leanpub.

Buy me an Espresso